Chimie des solutions
Cinétique chimique
Distillation
Procédés de séparation
Polymérisation
Électrolyse
Traitement eau
© The scientific sentence. 2007
| |
| Chimie: Procédés de séparation
1. Introduction:
Une filtration, une décantation ou une distillation sont des moyens de séparer les
constituants d'un mélange. Il existe aussi d'autres procédés de séparation dit d'extraction
qui consistent à faire passer un mélange dans un solvant de phase différente. On distingue:
| Mélange | Solvant | Type de séparation |
| liquide | gas | strippage |
| gas | liquide | absorption |
| liquide | solide | adsorption |
| solide | liquide | lixiviation |
| solide | solide | filtration |
| liquide | liquide | extraction liquide-liquide |
Tous ces procédés ont pour but de transférer le soluté du mélange vers le solvant.
Ce déplacement de soluté est appelé transfert de masse du mélange de soluté et
de diluant vers le solvant dans le but de maximiser la récupération
du soluté ou la purification du diluant. Le choix de la nature du solvant requiet une importance toute particulière du fait qu'il soit immiscible avec le diluant et que le soluté doit avoir une affinité pour ce solvant.
Ce mécanisme de transfert se déroule sur l'interface mélange-solvant, anisi l'agitation favorise le transfert de masse. L'extraction du solvant à partir du mélange vers le solvant se déroule à une vitesse decroissante jusqu'a ce que la concentration du soluté dans le diluant d'une part et dans le solvant d'autre part ne varie plus. Ainsi, dans cet état d'équilibre, la concentration initiale du soluté dans le mélange est partagée entre le diluant
et le solvant. Les concentrations de ces deux derniers à l'équilibre sont alors proportionnelles. Le coefficient de proportionnalité est appelé coefficient de partage qui ne dépend que de la température.
Ce procédé de séparation fait donc intervenir trois élements: le diluant,
le soluté et le solvant; le mélange initial diluant+soluté est appelé charge. L'extrait obtenu constitué du solvant et du soluté peut être conduit immédiatement vers un regénérateur (ou séparateur) pour obtenir un solvant pur prêt à être réutilisé, en circuit fermé, une seconde fois comme solvant d'extraction. Le solvant, dans tout le mécanisme de transfert ne joue qu'un
rôle intermédiare. Naturellement, la séparation proprement dite de se fait qu'après mélange intime de
la charge et du solvant.
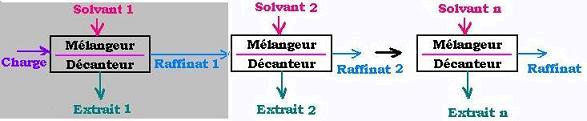
Pratiquement, un extracteur se compose d'un mélangeur et
d'un décanteur. Dépendemment du mélange à séparer, on utilise une extraction simple (un
seul extracteur)ou multiple (plusieurs extracteurs en série), ou en colonne (plateaux de plusieurs
extracteurs en parallèles avec une circulation charge-Solvant contre-courent. )
| Force centrifuge | Gravité | |
| Le lourd descend, le léger monte. | Colonne avec apport d'energie |
Colonne sans apport d'energie |
| | à extracteur | de dispersion |
| | à agitateurs rotatifs | à chicannes |
| | à pulsation | à plateaux perforés |
| | | à garnissage |
Selon le type de procédé à
séparer, en industrie on utilise une variété d'extracteurs classées initialement en deux
grandes catégories:
Ces procédés font intervenir le débit du mélange soluté + diluant apppelé charge,
qui en contact avec le débit du solvant engendre un débit riche en soluté appelé extrait
et un débit dépourvu de soluté appelé raffinat.
Rappelons enfin qu'un diluant abaisse la concentration dans un mélange et qu'un solvant
dissolve un soluté dans la solution. Le procédé d'extraction peut se schématiser ainsi:
(Charge = diluant + soluté) + solvant → (Extrait = soluté + solvant) + diluant
2. Extraction liquide-liquide:
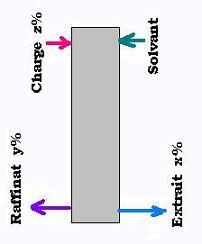
Nous avons:
F est le débit de charge et z% sa concentration masse-masse ent soluté.
S est le débit du solvant.
R est le débit du raffinat de concentration masse-masse y% en soluté.
Ex est le débit de l'extrait de concentration masse-masse x% en soluté.
Nous faisons les deux approsimations suivantes:
1. Le diluant et le solvant sont totalement immiscibles.
2. La charge est faiblement concentré en soluté.
Par conséquent: F = R et S = Ex
2.1 Bilan matière pour une extraction simple
Le bilan en débit de matière en soluté à travers un extracteur peut s'ecrire:
zF = yF + xS ou (z - y) F = x S (1.)
On défini deux paramètres:
- Le facteur d'extraction : rapprort entre le débit de soluté dans l'extrait et
le débit de soluté en raffinat: FE = E = xS/yF. En introduisant la constante de
partage K = x/y, on a : E = KS/F.
FE = E = xS/yF = KS/F, avec K = x/y (2.)
- Le taux d'extraction ou le rendement d'extractin: rapprort entre le débit de soluté dans l'extrait et
le débit de soluté dans la charge: TE = r = xS/zF. En introduisant la relation (1.), on obtient:
TE = r = (z - y) F/zF = 1 - y/z
TE = r = (z - y) F/zF = 1 - y/z (3.)
L'équation (1.) donne:
z = y + xS/F = y + y (xS/yF) = y + yE = y(1 + E) → y/z = 1/(1 + E)
y/z = 1/(1 + E) (4.)
2.2 Bilan matière pour une extraction multiple
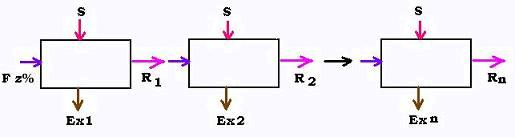
Dans ce cas, la concentration y% en soluté dans le raffinat reprend la place
de z et ainsi de suite jusqu'à la sortie.
Puisque y1/z = 1 /(1 + E) avec E = KS/F pour une première extraction , alors
pour une deuxième: y2/y1 = 1 /(1 + E).
Donc: y2/z = 1/(1 + E)y2
Par conséquent,
yn/z = 1/(1 + E)yn, avec E = KS/F (5.)
Si l'alimentation en S sur chaque extracteur est S/n, c'est à dire
provenant d'une source fornissant S est subdivisée par la suite également
sur chaque extracteur, la relation (5.) reste valable avec E = KS/nF.
Exemple:
Un extracteur effectue 3 extractions successives. Le débit de charge F = 90 kg/min,
la concentration en soluté z de la chrage est z = 0.75%, le débit du solvant
S est de 150 kg/min, et la constante de partage est de 2.2.
On veut calculer la teneur (concentration) en soluté y dans le raffinat
à la sortie de chaque extracteur:
Le débit S est partagé en trois sur chaque extracteur en série.
E = KS/3F = (2.2 x 150)/(3 x 90) = 1.22 → 1 + E = 2.22
1. Sortie de l'extracteur 1: yn = z /(1 + E)1 = 0.75/2.22 = 0.34%
2. Sortie de l'extracteur 2: y2 = z /(1 + E)2 = 0.75(2.22)2 = 0.15%
3. Sortie de l'extracteur 3: y3 = z /(1 + E)3 = 0.75(2.22)1 = 0.07%
Plus le nombre d'extracteur augmente, plus le raffinat s'appauvrie en soluté.
2.3 Bilan matière pour une colonne
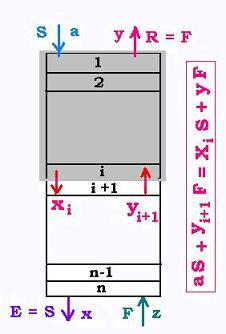
Le débit du solvant est S d'une teneur a d'impuretés. On suppose que le solvant est pur, ainsi a = 0. Le solvant rentre dans la colonne par la plateau 1. La variable de concentration en soluté dans S est x. À l'étage 0 elle vaut a , à l'étage 1 elle vaut x1; à l'étage i elle vaut xi; au dernier étage ellevaut xn, et à l'étage n+1, c'est à dire à la sortie, elle vaut xn+1 = x.
Le débit de l'extrait E, supposé égal à celui du solvant S sort de la colonne avec une concentration x en soluté.
Le débit de charge F constituée de diluant et de solut rentre dans la colonne avec une concentration z en soluté.
Le débit de raffinat R, supposé égal à celui de la charge sort de la colonne avec une tenneur y de soluté.
La variable de concentration en soluté dans F est y. À l'étage n+1, c'est à dire avant l'entrée elle vaut z , à l'étage d'entrée n elle vaut yn; à l'étage i+1 elle vaut yi+1; au premier étage elle vaut y1, et à l'étage 0, c'est à dire à la sortie, elle vaut yn+1 = y.
L'égalité entre les débits de soluté s'exprime par:
Ce qui rentre est égal à se qui sort. Elle est vrai aussi si on isole la partie de la colonne jusqu'au ième plateau.
Elle s'ecrit:
a S + yi+1 F = xi S + y F
(Eq. 1)
l'équation (Eq.1) donne:
yi+1 = xi (S/F) + y - a (S/F)
(Eq. 2)
Le coefficient de partage lors d'une séparation dans une colonne à plateux n'assure plus la proportionnalité entre les teneurs en soluté dans S et F. On montre que la relation entre ces teneurs est du type:
yi = m xi + b.
L'équation (Eq. 2) devient:
yi+1 = [yi - b](S/mF) + y - a (S/F)
On pose:
S/mF = E, donc:
yi+1 = E [yi - b] + y - a (S/F)
= E yi + y - b E - a mE (Eq. 3)
On pose aussi: am + b = y0.
Puisqu'on suppose que S est pur, y0 = b
Ainsi:
yi+1 = E yi + y - Ey0
(Eq. 4)
* i = 0 → y1 = E y0 + y - Ey0 = y (sortie du raffinat).
y1 = y .
* i = 1 → y2 = E y1 + y - Ey0
= E [y] + y - Ey0 = y(1 + E) - E y0
* i = 2 → y3 = E y2 + y - Ey0
= E [y(1 + E ) - E y0 ] + y - Ey0
= y(E + E2 ) - E2 y0] + y - Ey0 = y(1 + E + E2) - (E + E2 y0)
....
* i = n → yn+1 = y(1 + E + E2 + E3 + ... + En) - (E + E2 + E3 + ... + En)y0
La serie en E s'ecrit:
1 + E + E2 + E3 + ... + En = (En+1 - 1)/(E - 1)
(Eq. 5)
Il vient:
yn+1 = y(En+1 - 1)/(E - 1) - [(En+1 - E)/(E - 1)]y0
En négligeant la valeur de y0 = b, le deuxième terme disparait. Il reste
yn+1 = y(En+1 - 1)/(E - 1)
On a : yn+1 = z, donc:
y/z = (E - 1)/(En+1 - 1) (Eq. 6)
y est la teneur en soluté dans le raffinat en sortie de colonne. z est celle de la
charge à l'entrée de la colonne. E = S/mF est le coefficient transfert où m le coefficient
de partage d'un plateau de colonne, et n est le nombre de plateaux dans le colonne de
séparation.
Exemple:
Pour un débit de solvant S = 200.0 kg/min, un débit de charge F = 50.0 kg/min, un
coefficient de partage m = 2.0, et un rendement visé r = 95%, in faut un nombre n de
plateaux dans la colonne tel que:
r = 1 - (y/z) = 1 - (E - 1)/(En+1 - 1) = (En+1 - E)/(En+1 - 1)
En+1 - E = r (En+1 - 1)
En+1 ( 1 - r) = E - r
En+1 = (E - r)/(1 - r)
(n + 1) ln E = ln [(E - r)/(1 - r)]
n ln E = ln [(E - r)/(1 - r)] - ln E = ln [(E - r)/E(1 - r)]
n = ln [(E - r)/(1 - r)] - ln E
n = ln [(E - r)/E(1 - r)] / ln E
(Eq. 7)
E = S/mF = 200.0/2 x 50.0 = 2.0
n = ln [(2.0 - 0.95)/2.0 x (1 - 0.95)]/ ln 2.0 = 2.35/ 0.69 = 3 plateaux.
|

