Chimie des solutions
Cinétique chimique
Distillation
Procédés de séparation
Polymérisation
Électrolyse
Traitement eau
© The scientific sentence. 2007
| |
|
Chimie: Stoechiométrie
1. Introduction:
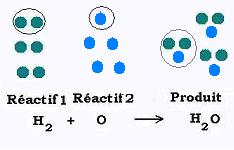
Théoriquement, dans une réaction chimique équilibrée, on s'interesse aux nombre d'atomes ou de molécules .
Les expressions suivantes sont équivalentes:
* Deux atomes d'hydrogène (H) se combinent avec un atome d'oxygène (O)pour former une molécule d'eau H2O.
* Une molécule d'hydrogène (H2) se combine avec un atome d'oxygène (O) pour former une molécule d'eau H2O.
* Deux moles d'atomes d'hydrogène (H) se combinent avec une mole d'atomes d'oxygène (O) pour former une mole de molécules d'eau H2O.
* Une mole de molécules d'hydrogène (H2) réagi avec une mole d'atomes d'oxygène (O) pour former une mole de molécules d'eau H2O.
 Dans une expérience au laboratoire, on a affaire à des grammes de substances; en industrie,
dans les réacteurs, les réactions chimiques se réalisent en tonnes de substances. On part
donc des masses de substances, qu'il faut convertir en moles pour pouvoir travailler
en proportions effectives. Bien entendu, une réaction chimique qui est équilibrée en termes de
molécules l'est aussi en termes de moles, il suffit juste de multiplier les deux membres de la réaction
par le nombre d'Avogadro pour passer des molécules aux moles. L'étude des réactions chimiques impliquant
les moles ou les masses est appelé Stoechiometrie.
Dans une expérience au laboratoire, on a affaire à des grammes de substances; en industrie,
dans les réacteurs, les réactions chimiques se réalisent en tonnes de substances. On part
donc des masses de substances, qu'il faut convertir en moles pour pouvoir travailler
en proportions effectives. Bien entendu, une réaction chimique qui est équilibrée en termes de
molécules l'est aussi en termes de moles, il suffit juste de multiplier les deux membres de la réaction
par le nombre d'Avogadro pour passer des molécules aux moles. L'étude des réactions chimiques impliquant
les moles ou les masses est appelé Stoechiometrie.
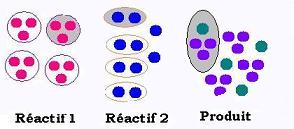
Pronons 12 boules rouges et 10 boules bleues. Chaque boule représente une mole. La nature d'une réaction
veut que trois moles rouges doivent se combiner avec 2 moles bleues pour former 1 mole verte et 3 moles violettes. On peut donc ecrire une réaction de cette sorte:
3 (moles R) + 2 (moles B) →
1(mole verte) + 3 (moles violettes)
Les coéfficients 3,2,1, et 3 sont appelés coéfficients stoechiométriques.
3 moles rouges doivent se rassembler dans le réactif 1 et 2 moles bleues dans
le réactif 2 pour se combiner et se transformer.
Le nombre d'un ensemble de trois moles dans le réactif 1 est égal à: 12/3 = 4. Celui de deux moles dans le réactif 2 est égal à 10/2 = 5.
Il ne va rien rester (12 - 3 x 4 = 0) comme moles rouges dans le réactif 1; elles vont toutes réagir. 4 x 3 moles rouges vont réagir avec 4 x 2 moles bleues.
Il va rester 10 - 2 x 4 = 2 moles bleues pour le réactif 2 qui ne réagiront pas.
Le nombre d'un ensemble pour le réactif 1 (= 4) est plus petit que celui dans le réactif 2 (qui vaut 5). On dit que le réactif 1 est limitant et le réactif 2 est en excès.
3 x 4 moles rouges réagiront: 12 - 3 x 4 = 0. On dit que la variation est égale à - 3x4.
2 x 4 moles bleues réagiront: 10 - 2 x 4 = 0 + 2. On dit que la variation est égale à - 2 x 4, avec un reste égal à 2.
La disparition de 3 moles rouges et de 2 moles bleues donneront 1 mole verte et 3 moles violettes.
Les moles rouges sont limitantes, 4 x 3 moles rouges disparaissent complètement, se combinant avec 4 x 2 moles blueus (reste 2) pour former 4 x 1 moles vertes et 4 x 3 moles violettes.
2. Definitions
On consiéere la réaction chimique suivante:
aA + bB → cC + dD
a moles de A vont réagir avec b moles de B pour former c moles
de C et d moles de D.
Si au départ nous avons X moles de A et Y moles de B, toutes
les moles de A ne réagiront pas avec toutes les moles de B
pour former de moles de C et des moles de D.
Seulement xa moles de A réagiront avec xb moles de B. On aura
donc:
xa = X et xb = Y
d'où
X/a = Y/b = x
Le plus petit des (X - xa) et (Y - xb) qui disparaisse le
premier est le limitant qui constitue la molécule
de référence.
Supposons que c'est la molécule A qui est le limitant, c'est
à dire toutes les molécules X = xa ont réagi. Si a moles de
A devront donner c moles de C et d moles de d, alors avec
xa moles de A, nous aurons xc moles de C et x d moles de D.
xa moles de A et xb moles de B disparaitront pour donner
xc moles de C et xd moles de D. Il restera Y - xb moles de B.
- xa et - xb → xc de C et xd de D
0 et (Y - xb) → xc de C et xd de D
| La réaction | a A + | b B → |
c C + | d D |
| Quantités initiales | X | Y | 0 | 0 |
| Limitant (sans reste) | X = xa | Y = xb + resteB | 0 | 0 |
| Reste | X - xa = 0 | Y - xb = resteB | xc | xd |
| Quantités finales | 0 | resteB | xc | xd |
3.Généralisations
Si l'on ecrit: X = (Moles de A) et Y = (Moles de B) les moles des réactifs,
et (Moles de C) et (Moles de D) les moles du produit, on peut ecrire:
x = (Moles de A)/a = (Moles de B)/b + [ResteB] = (Moles de C)/c = (Moles de D)/d
Règle:
(Moles de A)/a < (Moles de B)/b
A est le limitant et B est en excès et inversement.
Si les réactifs A et B sont en proportions stoechiométriques,
on aura ResteB = 0
x = (Moles de A)/a = (Moles de B)/b
= (Moles de C)/c = (Moles de D)/d
4. Taux de conversion
Si l'on veut arreter la réaction lorsque le réactif A (Mole de A)i
aurait atteint une certaine valeur (Mole de A)f; il restera
des moles du réactif (Moles de B) qui n'auront pas réagi. On parle du
taux de convversion du réactif A qu'on note αA:
αA= 100 x [(Moles de A)i - (Moles de A)f]/(Moles de A)i
i signifie initial, f signifie final.
5. Pourcentage molaire en excès
Revenons au cas de la réaction où A est limitant et
B est en excès. Lorsque le réactif A est épuisé , il restera
des moles de B qui n'ont pas réagi. On a:
(Moles de B)restantes = (Moles de B)i - (Moles de B)réagi
= (Moles de B)i - bx = (Moles de B)i - (Moles de A)i (b/a)
Om défini le pourcentage en excès βB du réactif B le rapport des moles
de B restantes et le nombre de moles qui ont réagi.
βB = (Moles de B)restantes)/(Moles de B)réagi =
= [(Moles de B)i - (Moles de B)réagi ]/(Moles de B)réagi
= [(Moles de B)i - (Moles de A)i (b/a)]/(Moles de A)i (b/a)
= [(Moles de B)i/b - (Moles de A)i /a ]/(Moles de A)i (1/a)
βB = [(Moles de B)i/b - (Moles de A)i/a ]/(Moles de A)i/a
ou
βB = [(a/b) (Moles de Bi/Moles de Ai)] - 1
6. Exemple 1
Soit la réaction de l'acide sulfurique H2SO4 avec la soude
caustique NaOH(hydroxyde de sodium) qui produit du sulfate de sodium et de l'eau.
Équilibrée, cette équation s'ecrit:
H2SO4 + 2 NaOH → Na2SO4 + 2H2O
Si l'on utilise 10 moles d'acide et 36 moles de soude.
La première chose à faire, c'est de trouver le limitant.
Acide: 10 - 1. x = 0 → x = 10
Soude: 36 - 2. x = 0 → x = 18
On a: 10/1 < 36/2 → l'acide sulfirique est le limitant.
Le réactif limitant est l'élement maitre pour le calcul de toutes
les proportions.
Une mole d'acide a besoin de deux moles de soude pour faire une
réaction, 10 en necéssiteront 20, il restera 36 - 20 = 16 moles de
soude non utilisées.
Comme une mole d'acide donnera une mole de sulfate, nous aurons
10 moles de sulfate de sodium dans le produit.
Comme une mole d'acide donnera deux moles d'eau, nous aurons
10.2 = 20 moles d'eau dans le produit.
Le pourcentage molaire en excès de la soude est:
βB = [(Moles de B)i /b - (Moles de A)i/a]/(Moles de A)i b/a)
βsoude= [(Moles de soude)i /b - (Moles d'acide)i/a ]/(Moles d'acide)i b/a)
= [36/2 - 10/1]/(10/1)= 0.8 = 80%
Si l'on arrête la réation lorsque 7 moles d'acide auraient réagi,
le taux de conversion de l'acide est:
αA= 100 x [(Moles de A)i - (Moles de A)f]/(Moles de A)i
αA= 100 x (Moles de A qui ont réagi)/(Moles de A)i
αacide = 100 x[7]/10 = 70%
7. Exemple 2
On cosière la réaction suivante:
2A + 3B → 5C + 7D
avec 10 moles de A et 12 moles de B.
Le limitant first!
A: 10 - 2x = 0 → x = 5
B: 12 - 3x = 0 → x = 4 ← c'est lui.
12 = 3 x 4, moles de B auront toutes réagi avec 2 x 4 = 8 moles de A.
Il restera donc 10 - 8 = 2 moles de A
Si l'on arrete la réaction lorsque le taux de conversion de B est 80%,
on aura:
αB= 80% = 100 x [(Moles de B)i - (Moles de B)f]/(Moles de B)i)
Donc:
(80%/100)(Moles de B)i) = (Moles de B)i - (Moles de B)f, d'où:
(Moles de B)f = (20%) (Moles de B)i = 20% x 12 = 2.4
Il y avait 12 moles de B au départ; donc 12 - 2.4 = 9.6 moles on réagi.
À ces 9.6 moles de B correspondent (9.6/3)x 2 = 6.4 moles de A et (9.6/3)x 5 = 16
moles de C et (9.6/3)x 7 = 22.4 moles de D,
selon les proportions stoechiométriques suivantes:
(Moles de A qui ont réagi)/a =(Moles de B qui ont réagi)/b
= (Moles de C produites)/c = (Moles de D produites)/d
Résumons tous ces chiffres dans un tableau:
| La réaction | 2 A + | 3 B → |
5 C + | 7 D |
| Quantités initiales (moles) | 10 | 12 | 0 | 0 |
| αB = 80% | | | | |
| Moles qui ont réagi | 6.4 | 9.6 | | |
| Moles produites | | | 16 | 22.4 |
| Moles restantes sans réaction | 10 - 6.4 = 3.6 | 12 - 9.6 = 2.4 | 0 | 0 |
8. Exemple 3
Dans un réacteur, on a la réaction suivante:
2 A + 3 B → 2 C + 2 D
La charge du réacteur est la suivante:
A : Volume = 1000 L à 2.5 mol/L.
Masse molaire = 20 g/mol.
B: Masse = 80 kg; masse molaire = 30 g/mol.
C: Masse molaire = 28 g/mol.
Volume(A) = 1000 L à 2.5 mol/L → Nombre de moles = 2500 moles.
B: Masse = 80 kg; masse molaire = 30 g/mol → Nombre de moles =
Masse/Masse molaire = 80,000/30 moles = 2667 moles.
Le limitant?
(Moles A)/a = 2500/2 = 1250 moles
(Moles B)/b = 2667/3 = 889 moles
Donc: B est le limitant.
Seules les 2 x 889 = 1778 moles de A vont réagir : 2500 - 1778 = 722 vont rester.
Les produits formé seront 2x 889 = 1778 pour C et pour D.
On le tableau suivant:
| | 2 A | 3 B | → | 2 C | 2 D |
| Initiales | 2500 | 2667 | | 0 | 0 |
| variations | - 1778 | - 2667 | | + 1778 | + 1778 |
| Finales | 722 | 0 | | + 1778 | + 1778 |
Si l'on arrête la réaction lorsque le taux de conversion de B
est de 80%, on aura:
αB= 100 x [(Moles de B)i - (Moles de B)f]/(Moles de B)i
Donc: [2667 - (Moles de B)f]/2667 = 0.80 → [2667 - (Moles de B)f]
= 2133.6 moles qui ont réagi, ou (Moles de B)f = 533.4 moles qui vont rester.
2133.6/3 = 711.2 toujours < (Moles A)/a = 2500/2 = 1250 moles
B est toujours limitant.
2133.6 moles de B vont réagir,
711.2 x 2 = 1422.4 moles de A vont réagir, 2500 - 1422 = 1078 vont rester,
711.2 x 2 = 1422.4 moles de C vont se produire,
711.2 x 2 = 1422.4 moles de A vont se produire,
On le tableau suivant:
| | 2 A | 3 B | → | 2 C | 2 D |
| Initiales | 2500 | 2667 | | 0 | 0 |
| variations | - 1422 | - 2134 | | + 1422 | + 1422 |
| Finales | 1078 | 533 | | + 1422 | + 1422 |
En termes de masse:
| | 2 A | 3 B | → | 2 C | 2 D |
| Initiales (Kg) | 2500 x 20 = 50 | 2667 x 30 = 80 | | 0 | 0 |
| Finales (Kg) | 1078 x 20 = 21.6 | 533 x 30 = 16 | | + 1422 x 28 = 39.8 | + 1422 x M(D) |
Utilisant la conservation de la masse, on aura:
50 + 80 = 21.6 + 16 + 39.8 + 1.422 x M(D) → = M(D) = 37 g/mol, qui
est la masse molaire de la substance D.
9. Exemple 4
On considère la réaction suivante:
A + 3 B → 2P
servant à produire 5 tonnes de produit P
La réaction doit s'effectuer dans les conditions suivantes:
Taux de conversion de A αA = 80%,
Pourcentatge molaire en excès de B est βB = 20%
Les masses molaires des substances sont: M(A)= 80 g/mol, M(B)= 40 g/mol, et
M(P)= 100 g/mol .
αA = (Moles de A qui ont réagi)/(Moles de A initiales) = 0.8 (1)
βB = [(a/b) (Moles de Bi/Moles de Ai)] - 1 = 0.20, ou
0.20 = [(1/3) (Moles de Bi/Moles de Ai)] - 1
Donc: (Moles de B initiales)/(Moles de A initiales) = 3 x 1.20 = 3.60 (2)
d'où (Moles de B initiales)/3 = (Moles de A initiales) x 1.20
Ainsi: (Moles de A initiales)/1 < (Moles de B initiales)/3 → A est limitant
D'autre part,
Moles de P = 5 x 106/100 = 5 x 104 moles.
Moles de P = 5 x 104 moles.
Ce nombre de moles produit est égal à 2Χ, où Χ est
la proportion stoechiométrique du limitant
= (Moles de initiales du limitant)/(Son coefficient dans la réaction)
= (Moles de initiales de A)/1
Donc: 2Χ = 5 x 104 → Χ = 25 x 103
d'où:
(1) → (Moles de A qui ont réagi) = 0.8 x (Moles de A initiales)= 25 x 103
Moles de A qui ont réagi = 25 x 103
D'où:
Moles de initiales de A = 25 x 103/0.8 = 31.25 x 103
(Moles de A restantes) = (Moles de A initiales) - (Moles de A qui ont réagi)=
31.25 x 103 - 25 x 103 = 6.25 x 103
Moles de A restantes = 6.25 x 103
(2) → (Moles de B initiales)
= 3.60 x (Moles de A initiales)= 3.60 x 31.25 x 103 = 112.5 x 103
Moles de B initiales = 112.5 x 103
Les moles de B qui ont réagi sont:
(Moles de B qui ont réagi) = bΧ = 25 x 103 x 3 = 75 x 103
Moles de B qui ont réagi = 75 x 103
(Moles de B initiales restantes) = (Moles de B initiales) - bΧ =
112.6 x 103 - bΧ = 112.5 x 103 - 25 x 103 x 3 = 87.5 x 103
Moles de B restantes= 87.5 x 103
On le tableau suivant (en Kmoles):
| | 1 A | 3 B | → | 2 P |
| Initiales | 31.25 | 112.5 | | 0 |
| variations | - 25 | - 75 | | + 50 |
| Finales | 6.25 | 37.5 | | 50 |
En termes de masse (en tonnes):
| | 1 A | 3 B | → | 2 P |
| Initiales | 31.25 x 80 = 2.5 | 112.5 x 40 = 4.5 | | 0 |
| Finales | 6.25 x 80 = 0.50 | 37.5 x 40 = 1.5 | | + 50 x 100 = 5 |
Le bilan matière donne:
2.5 -1.5 + 4.5 - 0.50 =? 5, le compte est bon.
10. Exemple 5
On veut réaliser 5 tonnes de produit P dans un réacteur à deux
cuvées selon une réaction à deux étapes comme suit:
A + 2 B → C
2 C + 2 D → 3 P
La réaction doit s'effectuer dans les conditions suivantes:
Taux de conversion de A αA = 80%,
Taux de conversion de C αC = 100%,
Pourcentatge molaire en excès de B est βB = 20%
Pourcentatge molaire en excès de D est βD = 10%
Les masses molaires des substances sont:
M(A)= 80 g/mol, M(B)= 40 g/mol, et M(D)= 65 g/mol .
Les taux de conversion:
αA = (Moles de A qui ont réagi)/(Moles de A initiales) = 0.80
αC = (Moles de C qui ont réagi)/(Moles de C initiales) = 1.00
Donc:
(Moles de A qui ont réagi) = 0.80 x (Moles de A initiales) (1)
(Moles de C qui ont réagi) = 1.00 x (Moles de C initiales) (2)
Les pourcentages molaires en excès:
βB = [(a/b) (Moles de B initiales)/Moles de A initiales)] - 1 = 0.20
Donc:
(Moles de B initiales)/(Moles de A initiales) = 1.20 x 2 = 2.40
βD = [(c/d) (Moles de D initiales)/Moles de C initiales)] - 1 = 0.10
Donc:
(Moles de D initiales)/(Moles de C initiales) = 1.10 x 1 = 1.10
Donc:
(Moles de B initiales) = 2.40 x (Moles de A initiales) (1')
(Moles de D initiales) = 1.10 x (Moles de C initiales) (2')
M(A) + 2M(B) = M(C)
2M(C) + 2M(D) = 3M(P)
M(P) = (1/3)[2M(A) + 4M(B) + 2M(D)] = (1/3)(2x80 + 4x40 + 2x65) = 150 g/mol
Moles du produit P = 5x106/150 = 33.33 kmoles
Moles de D = (2/3)Moles de P = 22.22 kmoles
Moles de C = (2/3)Moles de P = 22.22 kmoles
Taux de conversion de C αC = 1
Donc:
Moles initiales de C = Moles de C qui ont réagi = 22.22 kmoles.
Pourcentage molaire en excès de D βD = 10%
(2') donne: Moles de D initiales = 1.10 x (Moles de C initiales) = 24.44 kmoles
Les 22.22 kmoles de C viennent de la première réaction:
Donc:
Moles qui A ont réagi = 1 x 22.22 kmoles
Moles qui B ont réagi = 2 x 22.22 kmoles = 44.44 kmoles
Taux de conversion de A αA = 80%
(1) donne: Moles de A initiales = 22.22/0.80 = 27.78 kmoles
(1') donne: Moles de B initiales) = 2.40 x Moles de A initiales
= 2.40 x 27.78 = 66.67 kmoles
Masse de A qui a réagi = 22.22 x 80 = 1777.6 kg
Masse de A initiale = (Masse de A qui a réagi) /0.80 = 2222.0 kg
Moles initiales de A qui restent = 27.775 - 22.22 = 5.555 kMoles
Masse de A qui restent = 5.56 x 80 = 444.8 kg
Masse de B qui a réagi = 44.44 x 40 = 1777.6 kg
Masse de B initiale = 40 x 66.66 = 2666.40 kg
Moles de B qui restent = 66.66 - 44.44 = 22.22 kMoles
Masse initiale de D = M(D) x 24.442 kMoles = 1588.73 kg
Masse de D qui a réagi = 22.22 x 65 = 1444.30 kg
Moles de D qui retent = 24.442 - 22.22 = 2.22 kMoles
Masse de D qui restent = 2.22 x 65 = 144.30 kg
M(C) = M(A) + 2M(B) = 80 + 2x40 = 160 g/mol
Moles de C produit dans 1) = Moles de C initiales dans 2 =
Moles de C qui ont réagi dans 2 = 22.22 kMoles.
Donc: Masse de C produit dans 1, qui est épuisé dans 2 =
M(C) x 22.22 = 160 x 22.22 = 3555.20 kg
→ Masse initiale de C = 3555.20 kg
On les tableaux suivant (en Kmoles):
| | 1 A | 2 B | → | C |
| Initiales | 27.775 | 66.66 | | 0 |
| variations | - 22.22 | - 44.44 | | + 22.22 |
| Finales | 5.555 | 22.22 | | 22.22 |
| | 2C | 2 D | → | 3 P |
| Initiales | 22.22 | 24.442 | | 0 |
| variations | - 22.22 | - 22.22 | | + 33.33 |
| Finales | 0 | 2.22 | | 33.33 |
En termes de masse:
Masse de C qui a réagi + Masse de D qui a réagi =? Masse de P produit
Masse de C qui a réagi = Masse de A qui a réagi + Masse de B qui a réagi
= 1777.60 kg + 1777.60 kg = 3555.20 kg
Masse de D qui a réagi = 22.22 x 65 = 1444.30 kg
Donc:
Masse de C qui a réagi + Masse de D qui a réagi = 3555.20 kg + 1444.30 kg =
4999.5 = 5000 kg = Masse de P, le compte est bon.
|