Baccalauréats
Mathématiques
2013
Amérique du Nord
2005
Amérique du Nord
2007
Amérique du Nord
2012
Amérique du Nord
2010
Amérique du Nord
© The scientific sentence. 2010

|
Mathématiques :
Les baccalauréats
Bac S 2007 Amérique du nord corrigé
Corrigé du bac Mathématiques
S 2007 Amérique du nord
EXERCICE IV : 7 points
Commun à tous les candidats
1. Restitution organisée de connaissances.
a. Soit la fonction définie sur [0 ; +∞[
par
g(x) = exp{x} - x2/2
g est dérivable comme différence de fonctions
dérivables; pour tout x de [0 ; +∞[,
g'(x) = exp{x} - x > 0 puisque exp{x}> x pour tout x.
g'(x) est donc positif et g est croissante sur [0 ; +∞[;
g(0) = 1 donc, pour tout x > 0, g(x) > g (0) = 1.
donc g(x) > 0 .
b. On en déduit que, pour tout x ≥ 0, exp{x} ≥ x2/2.
Pour x > 0, en divisant par x, on obtient :
exp{x} /x ≥ x/2. Comme
lim x/2 = ∞ ,
x → ∞
d’après le pré-requis, on en déduit :
lim exp{x} /x = + ∞
x → ∞.
lim exp{x}/x = + ∞
x → ∞
2. Soit f la fonction définie sur [0 ; + ∞[ par
f(x) = (1/4) x exp{- x/2}.
a. La fonction exponentielle est positive sur [0 ; + ∞[
donc, pour tout x de [0 ; +∞[ , f(x) ≥ 0 .
b. Pour tout x ≥ 0, f (x) = (1/2)(1/2) x exp{- x/2}.
On pose X = x/2 . Donc
lim X = + ∞
x → + ∞
Par conséquent, d’après le théorème sur la
composition des limites, on a :
lim f(x) = lim (1/2) X exp {- X} = lim (1/2) X/exp {X}
x → + ∞
On a vu dans la question 1. que :
lim exp{x}/x = + ∞
x → + ∞
Donc
lim X/exp{X} = 0.
x → + ∞
Par conséquent :
lim f(x) = 0
x → + ∞
La courbe C admet donc une asymptote
d’équation y = 0 en +∞ .
c. f est dérivable sur [0 ; +∞[
comme produit et composée de fonctions dérivables.
On dérive et on obtient:
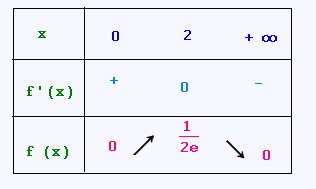
f'(x) = (1/5)(2 - x) exp{-x/2}
f'(x) = (1/5)(2 - x) exp{-x/2}
exp{-x/2} > 0, donc f'(x)
est du signe de 2 - x donc positif pour x ≤ 2, nul en 2 et
négatif pour x ≥ 2.
f est croissante sur [0 ; 2] et décroissante sur [2 ; +∞[.
Tableau de variations :
3. Soit F la fonction définie sur [0 ; +∞[ par:
F(x) = ∫(0,x) f(t) dt.
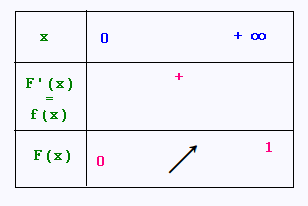
a. F est la primitive de f qui s’annule en 0 donc F' = f .
Comme on a montré que f était positive, F est
positive et F est croissante.
b. Pour tout x, F(x) = ∫(0,x)(1/4) t exp{-t/2}) dt.
Une intégration par parties donne:
F(x) = 1 - exp{-x/2} - (x/2) exp{-x/2}
c.
lim (-x/2) = - ∞
x → + ∞
Donc par composition avec la fonction exponentielle,
lim exp{- x/2} = 0
x → + ∞
Or , d'après ce qui précède:
lim (x/2) exp{- x/2} = 0
x → + ∞
Donc
lim F(x) = 1
x → + ∞
On en déduit le tableau de variations de F :
d. F est continue puisque dérivable; F est strictement
croissante; F(0) = 0 et
lim F(x) = 1
x → + ∞
D’après
le théorème des valeurs intermédiaires, il existe un unique
réel positif a tel que F(a) = 0.5.
À la calculatrice, on trouve : a ≈ 3.36 à 0.01 près par excès.
4. An = ∫(0,n) f(t) dt = F(n) - F(0) = F(n)
car F(0) = 0.
D’après la question précédente, le plus petit entier n
pour lequel An > 0.5 est n = 4 .
|
|