Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
|
Calculus: Rate of change of a function at the point
1. Rate of change of a function
f at the point a
1.1. Example
Consider a tree whose growth is defined by the function
f(t) = t2
t represents time in years,
f (t) represents the height the tree at time t, in feet.
Initially (t = 0), the height of the tree is
f(0) = 02 = 0
After a year (t = 1), the height of the tree becomes
f (1) = 12 = 1
...
For the first five years, we obtain:
f(0) = 02 = 0
f(1) = 12 = 1
f(2) = 22 = 4
f(3) = 32 = 9
f(4) = 42 = 16
f(5) = 52 = 25
Thus
from t = 0 to t = 1, the increase in height is 1 - 0 = 1,
from t = 3 to t = 5, the increase in height is 25 - 9 = 16
from t = a to t = b, the height of the tree will be increased f(b)- f(a).
The more interesting quantity, when we study the growth
of a function is the speed at which the growth occurs
on the given intervals. This quantity is called the average
rate of change of the function.
The average rate of change of the height of the tree
with respect to time:
from t = 0 to t = 2 is (4 - 1)/(2 - 0) = 1.5 feet/year
from t = 2 to t = 4 is (16 - 4)/(4 - 2) = 6 feet/year
from t = 3 to t = 5 is (25 - 9)/(5 - 3) = 8 feet/year
...
from t = a to t = b is (f(b) - f(a))/(b - a) feet/year
The average rate of change of a function f on the interval [a, b]
of its domain is given by:
(f(b) - f(a))/ (b - a)
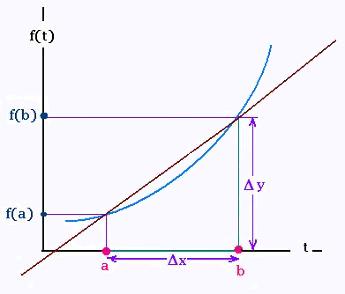In Geometry, the average rate of change of a function
on the interval [a, b], represents a slope.
The quantity : average rate of change corresponds to
the slope of the line through the two points
(a, f(a)) and (b, f(b)).
We write:
The average rate of change of f =
(variation of y)/(variation of x)
= Δy/Δx
1.2. Definitions
The average rate of change of a function f on the interval [a, b]
of its domain is given by:
(f(b) - f(a))/(b - a)
The average rate of change of f =
(variation of y)/(variation of x)
= Δy/Δx
2. Instantaneous rate of change of
a function
f at the point a
2.1. Example
Now, we want to know whether is possible to obtain the
growth rate of the height of the tree in a specific time, say
at the time t = 3 years.
First we approach the value t = 3 by considering
several average rates of change:
a) From the left
| t0 | (f(3) - f(t0))/(3 - t0) |
| 2.8 | 5.80 |
| 2.85 | 5.85 |
| 2.9 | 5.90 |
| 2.95 | 5.95 |
| 2.99 | 5.99 |
| 2.999 | 5.999 |
a) From the right
| t0 | (f(t0) - f(3))/(t0 - 3) |
| 3.2 | 6.20 |
| 3.1 | 6.10 |
| 3.05 | 6.05 |
| 3.02 | 6.02 |
| 3.01 | 6.01 |
| 3.001 | 6.001 |
We see that for the third year, the third
rate of growth will is very close to 6 feet/year.
We want to avoid using the calculator and all these lengthy
calculations each time and solve the problem by using the
notion of limit.
We proceed as follows:
a) We consider the time interval [3, t],
b) We find the average rate of change of the function on this interval,
Δy/Δt = (f(t) - f(3))/(t - 3)
c) We evaluate the limit as t approaches 3:
lim (f(t) - f(3))/(t - 3)
t → 3
Having f(t) = t2,
a)[t, 3] (t < 3) for which the average rate of change is:
(f(3) - f(t))/(3 - t)
lim (f(3) - f(t))/(3 - t)
t → 3-
= lim (9 - t2)/(3 - t) = 0/0: Indetermined.
t → 3-
=
lim (3 - t)(3 + t)/(t - 3) = 6
t → 3-
b) [3, t] (t > 3) for which the average rate of change is:
(f(t) - f(3))/(t - 3)
lim (f(t) - f(3))/(t - 3)
t → 3+
= lim (t2 - 9)/(t - 3) = 0/0: Indetermined.
t → 3+
=
lim (t - 3)(t + 3)/(t - 3) = 6
t → 3+
so
lim (f(t) - f(3))/(t - 3)
t → 3+
= lim (f(t) - f(3))/(t - 3)
t → 3-
= lim (f(t) - f(3))/(t - 3) = 6
t → 3
The obtained value 6 is called the instantaneous rate of change of
length of the tree on the third year.
2.2. Definitions
The instantaneous rate of change of a function f at x = a
on its domain is given by
lim (f(x) - f(a))/(x - a)
x → a
when this limit exists in R.
When we calculate the instantaneous rate of change of a function at a value
x = a, we calculate the slope of the line called the tangent line to the
the curve at the point x = a.
2.3. Other example
What is the rate of change of the function
f(x) = 2 x2 - 1
at
a) x = 1
b) = x = 2
a)
lim (f(x) - f(1) )/(x - 1)
x → 1
= lim ((2 x2 - 1) - (2 12 - 1))/(x - 1)
x → 1
= lim ((2 x2 - 1) - (1))/(x - 1)
x → 1
= lim 2(x2 - 1)/(x - 1) = 0/0: indetermined.
x → 1
= lim 2(x + 1) = 4
x → 1
b)
lim (f(x) - f(2) )/(x - 2)
x → 2
= lim ((2 x2 - 1) - (2 22 - 1))/(x - 2)
x → 2
= lim ((2 x2 - 1) - (7))/(x - 2)
x → 2
= lim (2x2 - 8)/(x - 2) = 0/0: indetermined.
x → 2
= lim 2(x2 - 4)/(x - 2) = lim 2(x + 2) = 8
x → 2
2.4. Other form of the rate of change of the function
2.4.1 Definition
We have;
Δ x = x - a
so
x = a + Δ x, and
x→ a is equivalent to Δ x → 0
Then:
(f(x) - f (a))/(x - a) = (f(a + Δ x) - f (a))/Δ x
Hence:
The rate of change of the function f
at the
point x = a on its domain is:
lim (f(x) - f (a))/(x - a)
x → a
|
= lim (f(a + Δ x) - f (a))/Δ x
Δ x → 0
|
We replace a by x to obtain:
The rate of change of the function f
at any
point x on its domain :
= lim (f(x + Δ x) - f (x))/Δ x
Δ x → 0
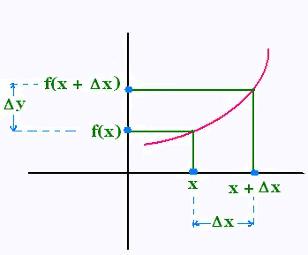
The rate of change of the function f
at any
point x on its domain is :
lim Δy/Δx
Δ x → 0
|
= lim (f(x + Δ x) - f (x))/Δ x
Δ x → 0
|
when this limit exists in R.
2.4.2 Example
What is the rate of change of the function
f(x) = 2 x2 - 1
at
a) x = 1
b) x = 30 ?
a)
lim Δy/Δx
Δ x → 0
= lim (f(x + Δ x) - f (x))/Δ x
Δ x → 0
= lim ((2 (x + Δx)2 - 1) - (2 x2 - 1)))/Δ x
Δ x → 0
= lim ((2 (x2 + 2 x Δx + Δ x2) - 1) - (2 x2 - 1)))/Δ x
Δ x → 0
= lim (4 x Δx + 2 Δ x2 )/Δ x
Δ x → 0
= lim (4 x + 2 Δ x ) = 4 x
Δ x → 0
At x = 1, we have:
lim (4 x + 2 Δ x ) = 4 . 1 = 4
Δ x → 0
That is the value found above.
b)
At x = 30, we have:
lim (4 x + 2 Δ x ) = 4 . 30 = 120
Δ x → 0
3. Exercices:
|
|
