Calculus I: Geometric Interpretation of the derivative

1. Slope and derivative

Let's draw some lines passing through two points on the curve of equation y = f(x):
one fixed of abscissa xo and another of abscissa x moving toward the fixed point.

As x approaches xo, the secant line becomes the tangent line at the end. Its slope "a" becomes equal to the derivative f'(xo) of the function y = f(x) at the point xo.

Geometrically, the slope "a" is equal to the average rate of change:
a = (yf - yi)(fx - xi)
yf and yi are any two ordinates corresponding to their abscissa xf and xi via the tangent line y = a x + b.

2. Derivative at a given point

By definition, for any point (xo, f(xo)) on the curve of the function f(x), the derivative at this point is:

f'(xo) =	lim (f(x) - f(xo))/(x - xo)	= lim Δf(x)/Δx
	x → o	Δx → o

This limit f'(xo) is the slope of the tangent line at this point.

The equation of the tangent line at the point (x0,f(xo)) on the curve of the function f(x) is :

y = a x + b

Where a = f '(xo).

Therefore

The equation of the tangent line at the point (xo, f(xo) on the curve of the function f(x) is :

y = f '(xo) + b

3. Example:

In the following figure, we have three tangent lines:


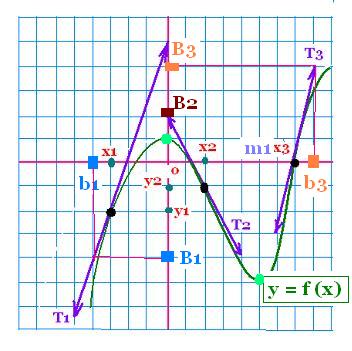
1) Tangent T1

Its equation is :

y = f '(x1) + b

f '(x1) is the slope of the tangent line T1 that we can find as follows:

f '(x1) = (B1 - y1)(b1 - x1)

By taking any two points on this tangent.

Example:

f'(x1) = (B1 - y1)(b1 - x1) = ((- 4) - 2)/(4 - 3) = - 6


2) Tangent T2

Its equation is :

y = f '(x2) + b

f '(x2) is the slope of the tangent line T2 that we can find as follows:

f '(x2) = (B2 - y2)(b2 - x2)

By taking any two points on this tangent.

Example:

f '(x2) = (B2 - y2)(b2 - x2) = (2 - 0)/(0 - 2) = 2/(- 2) = - 1


3) Tangent T3

Its equation is :

y = f'(x3) + b

f '(x3) is the slope of the tangent line T3 that we can find as follows:

f '(x3) = (B3 - y3)(b3 - x3)

By taking any two points on this tangent.

Example:

f '(x3) = ((4 - 0)(8 - 7) = 4/1 = 4