Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
| Calculus I: Concavity and inflection points
1. Concavity of a function
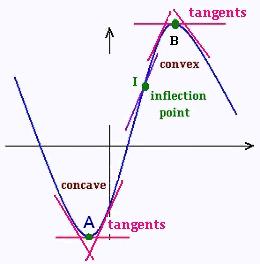
The graph of a function, in some region, can be
concave (concave up), as for the point A or
convex (concave down), as for the point B.
Around a point in a concave region, the slopes of
the tangents increases and the curve is above the tangents,
while the slopes of the tangents in the convex region
decreases and the curve is under the tangents.
At the point I, the concavity changes the direction. This
point is called the inflection point.
2. Definition of concavity of a function
We use second derivative of a function to
determine the shape of its graph.
Definition 1:
Let f a function differentiable on the neighborhood of
the point c in its domain.
a) If f"(c) > 0 then the graph of the function f is
concave at the point (c,f(c)).
b) If f"(c) < 0 then the graph of the function f is
convex at the point (c,f(c)).
Definition 2:
If f"(c) = 0 or f"(c) fails to exist, then the
graph of f is either concave or convex, or
neither the two of them.
Examples
Example 1
f(x) = 2 x3 - x + 1
f'(x) = 6 x2 - 1
f"(x) = 12 x
a) At the point c = - 4
f"(- 4 ) = - 48 < 0. So at this point the function
is convex.
b) At the point c = 0
f"(0) = 0. So at this point called the transition number
of the function f.
c) At the point c = + 2
f"(+ 2) = + 24 > 0. So at this point the function
is concave.
Example 2
f(x) = 1/x
f'(x) = - 1/x2
f"(x) = 2/x3
f"(0) 
Hence at the point 0, the graph of f is neither concave upward
nor concave downward because f"(0) does not exist.
3. Transistion and inflection point
If the point c is in the domain of the function f, and
f"(c) = 0 or f"(c) fails to exist, then the real c is called
transition mumber of the function f.
The transition is between concavities (upward or downward).
Example
f(x) = 2x4 - x3 + 5
f'(x) = 8 x3 - 3 x2
f"(x) = 24 x2 - 6 x
f"(0) = 0 with x = 0 or x = 1/4
The points c = 0 and c = 1/4 are included in
the domain of the function f; their second derivative
are zero, then they are the transition numbers
of the function f.
4. Concavity on an interval
Let f a differentiable function on an interval ]a, b[.
For any x in the interval ]a, b[:
a) If f"(x) > 0 then the graph of f is concave upward
in the whole interval ]a, b[.
b) If f"(x) < 0 then the graph of f is concave downward
in the whole interval ]a, b[.
Example
f(x) = x4 - 6 x2 + 5
f'(x) = 4 x3 - 12 x = 4 x (x2 - 3) =
4 x (x - √3)(x + √3)
f"(x) = 12 x2 - 12 = 12 (x + 1)(x - 1)
We have the following variation and sign table:
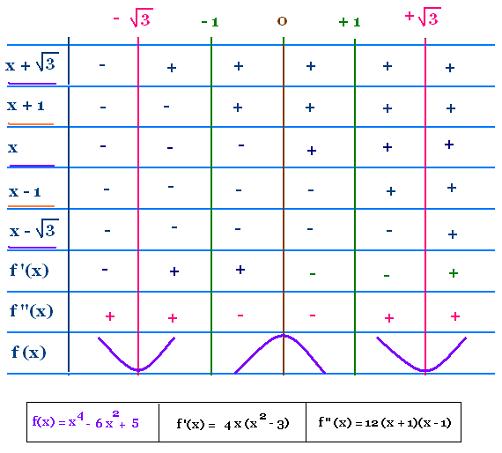
The domain of the function f is ℝ.
f'(x) = 4 x (x2 - 3) = 0
when x = 0, x = + √3, or x = - √3.
These three points are the maxima of the function f.
x = 0 is the maximum, and x = - √3, + √3
are the two minimum.
f"(x) = 12 (x + 1)(x - 1) = 0
when x = - 1 or x = + 1.
We don't have any point where f "(x)  Therefore the transition numbers are: {- 1, + 1}
Therefore the transition numbers are: {- 1, + 1}
The graph of the function f is concave upward in
the interval ]- ∞ - 1[ U ]+ 1, + ∞[,
and concave downward (convex) in
the interval ]- 1, + 1[.
5. Concavity and inflection point
Let f a function and c a point in its domaine.
If
a) The function f is contimuous at the point c, and
b) There is a shift in the concavity of the function f
either side of the point c (f "(x) changes its sign
either side of the point c),
Then
The point (c, f(c)) is an inflection point of the graph
of the function f at the point c.
If the point (c, f(c)) is an inflection point, then
c is a transition number of f. But the contrary is not true
because we can have f "(c) so c is a transition
point without being an inflexion point. so c is a transition
point without being an inflexion point.
Example
The function seen above
f(x) = x4 - 6 x2 + 5,
has two inflection points:
I1 = ( - 1, 0) and I1 = (+ 1, 0).
6. Second derivative and reltive extrema
Let f a function and c a point in its domaine.
The test of the first derivative with
crtitic points states:
If f(c) is a relative extremum of the function f,
then c is a critical point.
We can use the test of the second derivative instead.
Let f a function and c a point of its domain which
is critical.
If the function est differentiable two times at the point c,
that is if f " exist at this point, and this function
is continuous at this point, and
a) f "(c) > 0, then the point (c, f(c)) is a relative minimum of f
b) f "(c) < 0, then the point (c, f(c)) is a relative maximum of f.
Generally, the bottom of the concavity is a minimum, and
the top of the convexity is a maximum.
Example
The function seen above:
f(x) = x4 - 6 x2 + 5
f'(x) = 4 x (x - √3)(x + √3)
f"(x) = 12 x2 - 12
The critical points are c0 = 0, c1 = - √3 and
c2 = + √3.
We have
f "(c0) = f "(0) = 12 (0)2 - 12 = - 12
< 0 → this point is a relative maximum of f.
f "(c1) = f "(- √3) = 12 (- √3)2 - 12 = 24
> 0 → this point is a relative minimum of f.
f "(c2) = f "(+ √3) = 12 (+ √3)2 - 12 = 24
> 0 → this point is a relative minimum of f.
7. Exercices
|
|

