Calculus I: Inverse functions
Derivative
1.Definitions
The inverse function f-1 of a given function f(x)
is the function that returns the variable taken by the function f.
That is if f transforms x into y = f(x), then f-1(y) returns
x, i.e f-1(y) = x.
f(x) composed with g(x) leaves x unchanged.
Therefore, the relationship between the function f(x)
and its inverse g(y) (= f-1(y)) is
f(g(x)) = g(f(x)) = x.
g is the inverse of f :
f(g(x)) = g(f(x)) = x
2. Examples
f(x) = x2
g(x) = √x
f(x) = ax
g(x) = logax
f(x) = sin x
g(x) = arcsin x
3. Invertible functions
3.1.Definitions
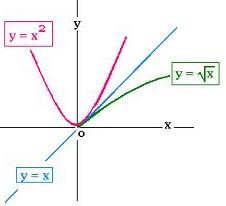
Not all functions are invertible, that is
have inverse.
The function f(x) = x2 has the same value
yo = f(xo) for two variables + xo and - xo.
Therefore
the inverse function f-1(yo) corresponds to
two values in the domain of f: + xo and - xo. Hence f-1(yo) is
not a function (just a relation).
A function must correspond to no more than one image (y) for each variable (x), which is called one-to-one function.
Even if a function f is not one-to-one, it is possible to restrict the domain.
For example, the function f(x) = x2 is not one-to-one.
By restricting the domain to R+ = [0, +∞[ (non-negative numbers), the function f becomes one-to-one (injective), hence invertible.
3.2. Examples: Trigonometric functions
Example 1: ArcSin(x)
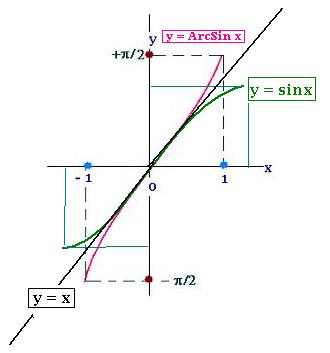
The sine function is not one-to-one. For a value y = sin(x), we have an infinity
of related numers, that is x ± 2kπ (for every integer n).
However, if we restrict the domain R to just [- π/2, + π/2],
the sine becomes is one-to-one, then invertible. The corresponding inverse function is
called arcsine and denoted Arc Sin or Sin-1 .
Arc Sin x stands for the arc on the cercle of radius 1, corresponding to a sine equal to 1, measured in
radians (or degrees).
y = arcsin x
x = sin y
- π/2 <= y <= +π/2
Example 2: ArcCos(x)
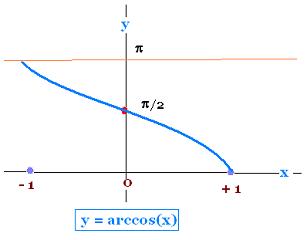
Similarly, we define arccosine Arc Cos or Cos-1 as
the inverse function of cosine Cos:
y = arccos x
x = cos y
0 <= y <= π
Example 3: Arctan(x)
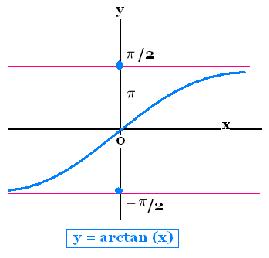
We define arcTan ArcTan or Tan-1 as
the inverse function of Tangent:
y = arctan x
x = tan y
- π/2 < y < +π/2
Example 4: Arccot(x)
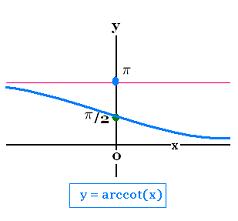
We define ArcCot or Cot-1 as
the inverse function of Cotangent:
y = arccot x
x = cot y
0< y < +π
4. Derivative of inverse functions
4.1. Definitions
We have
f(g(x)) = x
Using chain rule, we write:
(df(g(x))/dg(x)) . (dg(x)/dx) = dx/dx = 1
Or
(df(g)/dg) . g'(x) = 1
(df(g)/dg) . g'(x) = 1
4.2. Example: d(Arcsin x)/dx
Let f a function and g is its inverse. We have the following formula:
f(g(x)) = x, and
(df(g)/dg) . g'(x) = 1
Let:
y = g(x) = Arcsin x
so
x = sin y
f(g(x)) = sin [ArcSin(x)]
(d sin y/ dy ) . (d Arcsin x /dx) = dx/dx = 1
(cos y) . d Arcsin x)/dx = 1
d(Arcsin x)/dx = 1 /cos y = 1/(1 - sin2y)1/2 = 1/(1 - x2)1/2
d(Arcsin x)/dx = 1/(1 - x2)1/2
|

