Calculus I: Derivatives
Proof of some derivative properties
In this chapter, we�re going to prove many of the various derivative
properties, by using the definition:
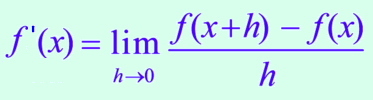
1. Continuity of a differentiable function
If f(x) is differentiable at x = a then f(x) is continuous at x = a .
f(x) is differentiable at x = a . So
lim ((f(x) - f(a))/(x - a) = f'(a)
x → a
We have if x ≠ a :
lim (f(x) - f(a)) = lim [(f(x) - f(a))/(x - a)] . lim (x - a) =
x → a
= f'(a) x 0 = 0
We have also :
lim f(x) = lim (f(x) - f(a) + f(a) ) =
x → a
lim (f(x) - f(a)) + lim f(a) = 0 + f(a) = f(a)
x → a
lim f(x) = f(a) → f is continuoous at x = a
x → a
2. Sum and difference of two functions
(f(x) ± g(x))' = f'(x) ± g'(x)
We have :
lim [(f(x + h) + g(x + h)) - (f(x) + g(x))]/h = (f(x) + g(x))' =
h → 0
lim [f(x + h) - f(x) + g(x + h)) - g(x)]/h =
h → 0
lim (f(x + h) - f(x))/h + lim (g(x + h) - g(x))/h =
h → 0
f'(x) + g'(x))
(f(x) ± g(x))' = f'(x) ± g'(x))
3. Constant times a function
(c f(x))' = c f'(x)
We have :
lim (c f(x + h) - c f(x))/h = c lim (f(x + h) - f(x))/h = c f'(x)
h → 0
(c f(x))' = c f'(x)
4. Derivative of a constant
(c)' = 0
We have :
lim (c - c )/h = 0 = lim 1/h = 0
h → 0
(c)' = 0
5. Product rule
(f g)' = f' g + f g'
We have :
lim (f(x + h) g(x + h) - f(x) g(x))/h =
h → 0
 hint : add and subtract f(x + h) g(x) hint : add and subtract f(x + h) g(x)
lim (f(x + h) g(x + h) - f(x) g(x) + f(x + h) g(x) - f(x + h) g(x))/h =
h → 0
lim (f(x + h) g(x + h) - f(x + h) g(x) - f(x) g(x) + f(x + h) g(x))/h =
h → 0
lim (f(x + h) (g(x + h) - g(x)) + g(x) (f(x + h) - f(x))) /h =
h → 0
lim (f(x + h) (g(x + h) - g(x)))/h + lim (g(x) (f(x + h) - f(x)))/h =
h → 0
f(x + 0) g'(x) + g(x) f'(x) = f(x) g'(x) + g(x) f'(x)
(f g)' = f' g + f g'
6. Quotient rule
(f/g)' = (f' g - f g')/g2
We have :
lim (f(x + h) / g(x + h) - f(x) / g(x))/ h =
h → 0
lim (1/h) (f(x + h) g(x) - f(x) g(x + h))/ g(x) g(x + h) =
h → 0
 hint : add and subtract f(x) g(x) hint : add and subtract f(x) g(x)
lim (1/h) (f(x + h) g(x) - f(x) g(x + h) + f(x) g(x) - f(x) g(x)
)/ g(x) g(x + h) =
h → 0
lim (1/h) (f(x + h) g(x) - f(x) g(x) + f(x) g(x) - f(x) g(x + h))
/ g(x) g(x + h) =
h → 0
lim (1/h) (g(x)(f(x + h) - f(x)) - f(x)(g(x + h) - g(x)))
/ g(x) g(x + h) =
h → 0
lim (g(x)(f(x + h) - f(x))/h - f(x)(g(x + h) - g(x))/h
/ g(x) g(x + h)) =
h → 0
(g(x)f'(x) - f(x)g'(x))
/ g(x) g(x + 0) =
(g(x)f'(x) - f(x)g'(x)) / (g(x))2
(f/g)' = (f'g) - fg')/g2
7. Power rule
(xn)' = n xn - 1
We can use three methods to prove this:
. Logarithmic differentiation,
. The derivative:
f'(a) = lim (f(x) - f(a))/(x - a), and
x → a
. The the binomial methode. Let's use this latter.
The binomial formula is :
(x + h)n = Σ (n, k) xn - k hk
Fom k = 0 to n .
Where
(n, k) = n!/k!(n - k)!
Then
lim ((x + h)n - xn) / h = f'(x) =
h → 0
(Σ (n, k) xn - khk - xn) / h =
h → 0
(xn + n xn - 1 h + ... + - xn) / h =
h → 0
(n xn - 1 + ... + ) = n xn - 1
(xn)' = n xn - 1
8. Chain rule
(f(g(x)))' = f'(g(x)) . g'(x)
F(x) = fog(x) = f(g(x))
F'(x) = f'(g(x)) . g'(x)
lim (F(x + h) - F(x))/h = F'(x) =
h → 0
lim ( f(g(x + h)) - f(g(x)) )/h =
h → 0
We are assuming that the function g(x) is differentiable
at the point x. That is the number g'(x) exists and is equal
to the limit definition of the derivative:
lim (g(x + h) - g(x))/h = g'(x)
h → 0
We are assuming also that the function f(x) is differentiable
at the point x. That is the number f'(x) exists and is equal
to the limit definition of the derivative:
lim (f(y + k) - f(y))/k = f'(y)
k → 0
Let's rewrite f(g(x + h)) at h NEAR 0 :
g(x + h) = h g'(x) + g(x)
f(y + k) = k f'(y) + f(y)
And replace it in :
lim ( f(g(x + h)) - f(g(x)) )/h = F'(x)
h → 0
So
lim (f(g(x) + h g'(x)) - f(g(x)) )/h
h → 0
Let's use f(y + k) = k f'(y) + f(y), therefore:
f(g(x) + h g'(x)) = h g'(x) f'(g(x)) + f(g(x))
lim ( (h g'(x) f'(g(x)) + f(g(x))) - f(g(x)) )/h =
h → 0
lim ( h g'(x) f'(g(x)) )/h = g'(x) f'(g(x))
h → 0
(f(g(x)))' = f'(g(x)) . g'(x)
|

