Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II: Riemann sum & integrals
1. Riemann sum
1.1. Definition
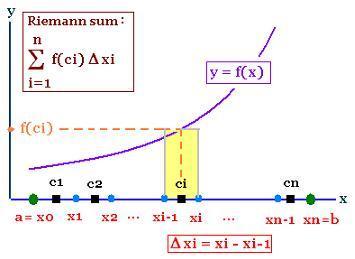
Let f a function continue on the interval [a,b].
We want to construct a sum of the function f as follow:
1. We subdivide the interval [a, b] into n sub-intervals and obtain the partition of this interval:
[x0 = a, x1], [x1, x2], [x2, x3], ..., [xi-1, xi], ..., [xn-1, xn].
The width of each sub-interval is equal to Δxi = xi - xi-1.
2. We choose a representative point ci inside each sub-interval: ci ∊ [xi-1, xi]
3. We perform the sum:
f(c1)Δx1 + f(c2)Δx2 + ... + f(ci)Δxi + ... + f(cn)Δxn =
Σi=1nf(ci)Δxi
This sum is called Riemann sum or integral sum of
the function f on the interval [a, b].
1.2. Example
What is the value of the Riemann sum of the function
f(x) = x2 + 1 on the interval; [2, 7]?
Let consider 5 sub-intervals with equal width Δxi equal to 1; and the mid-point of each sub-interval as its representative. Therefore
The partition is:
[x0 = 2, 3], [3, 4], [4, 5], [5, 6], [6,7]
The 5 representatives ci are:
2.5, 3.5, 4.5, 5.5, 6.5
The Riemann sum is:
Σi=15 f(ci)Δxi =
f(2.5)(1) + f(3.5)(1) + f(4.5)(1) + f(5.5)(1) + f(6.5)(1).
=
((2.5)2 + 1) + ((3.5)2 + 1) ((4.5)2 + 1) ((5.5)2 + 1) ((6.5)2 + 1).
= 6.25 + 12.25 + 20.25 + 30.25 + 42.25 + 5 = 116.25
f(x) = x2 + 1
Σi=15 f(ci)Δxi = 116.25
units2.
2. Definite integral
2.1. Definition
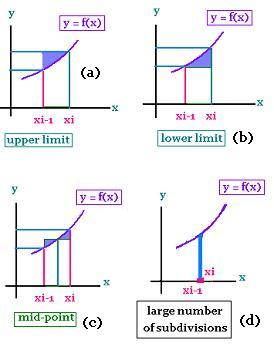
Note that the width of the sub-interval is not necessarily the same for all the intervals of the partition, and the representative point is not necessarily a midpoint.
The width of the sub-intervals are taken equal to make the calculations simple.
If we take the upper bound of the sub-interval instead of the midpoint we will gain the related triangle
in each sub-interval (a).
If we take the lower bound of the sub-interval instead of the midpoint we will lose the related triangle
in each sub-interval (b).
If we take the mid-point of the sub-interval we gain and loose the two related equal triangle. Therefore ,
the mid-point as a representative point is a good approximation (c).
The more the width of the sub-interval is small (Δx → 0), the more we approach the true value of the sum. This is obtained by taking a large number of subdivisions (d). In this case the position of the representative does not matter.
f is a function continue on the interval [a, b]
If lim Σi=1n f(ci)Δxi = A
max Δxi → 0
then the function f is integrable on the interval [a, b]. The value A of the limit is the definite integral of the function f on [a, b], denoted by:
Integral of f(x) dx from a to b.
While Δxi tends to zero, the value A does not depend on the representative within each sub-interval, and does not depend on the subdivision. To calculate the Riemann sum, it is therefore easier to take equal sub-intervals.
We have then: Δxi = (b - a)/n, and the definition of
definite integral becomes:
| | b | | | | | | n | |
| ∫ | | f(x) dx | = | limit | | | Σ | f(ci) Δxi |
| | a | | | n → ∞ | | | i=1 | |
2.2. Example
Value of the Riemann integral of f(x) = x2 + 1
The function f(x) is continuous in the interval [2, 7].
We subdivide the interval [2, 7] in n equal sub-intervals
of width Δxi = dx = (7 - 2)/n = 5/n.
xo = 2
x1 = xo + 5/n = 2 + 5/n
x2 = x1 + 5/n = 2 + 2(5/n)
x3 = x2 + 5/n = 2 + 3(5/n)
... = ...
xi = b = 2 + i(5/n) = 7
2.2.1. Representative point at the mid-point
The representative points are chosen as the mid-point
of sub-intervals:
c1 = (x0 + x1)/2 = (4 + 1 (5/n))/2
c2 = (x1 + x2)/2 = (4 + 3 (5/n))/2
c3 = (x2 + x3)/2 = (4 + 5 (5/n))/2
... = ...
ci = (xi-1 + xi)/2 = (4 + (2i - 1)(5/n))/2 = 2 + (2i - 1)(5/n)
... = ...
cn = (xn-1 + xn)/2
Σi=1n
f(ci)Δxi =
Σi=1n
f(2 + (2i - 1)(5/n))(5/n) =
(5/n) Σi=1n
f(2 + (2i - 1)(5/n))
f(2 + (2i - 1)(5/n)) = (2 + (2i - 1)(5/n))2 + 1 =
(4 - 10/n) +(20/n - 25/n2)i + (25/n2)i2 + 1
Therefore
Σi=1n f(2 + (2i - 1)(5/n))(5/n) =
(5/n) Σi=1n [(4 - 10/n) +(20/n - 25/n2)i
+ (25/n2)i2 + 1] =
Using the formulas:
Σi=1n E = n E
Σi=1n i = n(n + 1)/2
Σi=1n i2 = n(n + 1) (2n + 1)/6
we obtain:
Σi=1n
f(ci)Δxi =
(5/n) [n(4 - 10/n) +(20/n - 25/n2)n(n + 1)/2
+ (25/n2)n(n + 1) (2n +1)/6 + n] =
5 [(4 - 10/n) +(20/n - 25/n2)(n + 1)/2
+ (25/n2)(n + 1)(2n +1)/6 + n]
Now we evaluate the related limit:
lim Σi=1n f(ci)Δxi = 116.67
n → ∞
Hence
| |
7
| |
| ∫ | |
(x2 + 1) dx = 116.67 units2
|
| |
2
| |
2.2.2. Representative point at the upper bound
The representative points are chosen as the upper bound
of sub-intervals:
c1 = x1 = x0 + 5/n = 2 + 5/n
c2 = x2 = x1 + 5/n = x0 + 2 5/n = 2 + 2 5/n
c3 = x3 = x0 + 3 5/n = 2 + 3 5/n
... = ...
ci = = xi = 2 + 5i/n
... = ...
cn = = xn = 2 + n 5/n = 7
Σi=1n
f(ci)Δxi =
Σi=1n
f(2 + 5i/n)(5/n) =
(5/n) Σi=1n
f(2 + 5i/n)
f(2 + 5i/n) = (2 + 5i/n)2 + 1 = 5 + 20i/n + 25i2/n2
Therefore
Σi=1n f(2 + 5i/n) (5/n) =
(5/n) Σi=1n [5 + 20i/n + 25i2/n2] =
Using the formulas:
Σi=1n E = n E
Σi=1n i = n(n + 1)/2
Σi=1n i2 = n(n + 1) (2n + 1)/6
we obtain:
Σi=1n
f(ci)Δxi =
(5/n) [5 n + (20/n)n(n + 1)/2 + (25/n2)n(n +1 )(2n + 1)/6] =
5 [5 + (20/n)(n + 1)/2 + (25/n2)(n + 1)(2n + 1)/6]
Now we evaluate the related limit:
lim Σi=1n f(ci)Δxi = 5(5 + 10 + (25)(2)/6] = 116.67
n → ∞
Hence
| |
7
| |
| ∫ | |
(x2 + 1) dx = 116.67 units2
|
| |
2
| |
4. Exercises
|
|