Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II: Definite integral
Simpson's rule
In the last section, Trapezoidal Rule, we used straight lines to model a curve and learned that it was an improvement over
Using Rectangles method for finding areas under curves involves much
«missing » from each segment.
By Trapezoidal rule , we use straight lines to model a curve. It
involves much less «missing » from each segment. Il is
already an improvement over using rectangles method.
Now Simpson's rule is an even better approximation for
the area under a curve.
In Simpson's Rule, we will use parabolas to approximate each part of the curve. It is very efficient since it's generally more accurate than the Rectangles and Trapezoidal numerical methods.
Simpson's Rule
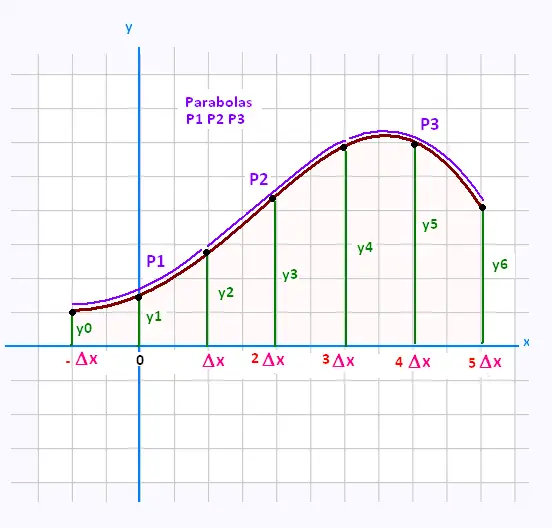
We divide the area under the curve into n areas with
equal segments of width Δx. The total approximate area is
the sum of these n parts.
As usual, the more divisions we take, the more accurate it will be.
Note: In Simpson's Rule, n must be EVEN.
We consider the area under the general parabola y = ax2 + b x + c.
Let's consider the first parabola P1. We have:
A1(x) = ∫ (ax2 + b x c) dx = a x3/3 + b x2/2 + c x + d
A1 = A1(+ Δx) - A1(- Δx) =
a (Δx)3/3 + b (Δx)2/2 + c (Δx) -
a (- Δx)3/3 - b (- Δx)2/2 - c (- Δx) =
2a (Δx)3/3 + 2 c (Δx)
A1 = (Δx/3)[2a (Δx)2 + 6 c]
We have also:
y0 = a (Δx)2 - b(Δx) + c
y1 = c
y2 = a (Δx)2 + b(Δx) + c
Therefore
y0 + y2 = 2 a(Δx)2 + 2 y1 , and
2a = (y0 + y2 - 2y1)/(Δx)2
Substituting these expressions of a and c into A = (Δx/3)[2a (Δx)2 + 6 c ]
yields:
A1 = (Δx/3)[((y0 + y2 - 2y1)/(Δx)2) (Δx)2 + 6 y1 ]
=
(Δx/3)[(y0 + y2 - 2y1) + 6 y1] = (Δx/3)(y0 + y2 + 4y1)
A1 = (Δx/3)(y0 + 4y1 + y2 )
The parabola P2 passing through the 3 points (Δx, y2),
(2Δx, y3), and (3Δx, y4), will have an area:
A2 = (Δx/3)(y2 + 4y3 + y4)
, and
the last part of parabola P3 will have
A3 = (Δx/3)(y4 + 4y5 + y6).
Therefore, the sum of the areas under the 3 resulting parabolas, for
6 subintervals is:
A = A1 + A2 + A3 = (Δx/3)(y0 + 4y1 + y2 ) +
(Δx/3)(y2 + 4y3 + y4) + (Δx/3)(y4 + 4y5 + y6) =
(Δx/3)(y0 + 4y1 + y2 + y2 + 4y3 + y4 + y4 + 4y5 + y6) =
(Δx/3)(y0 + 4(y1 + y3 + y5) + 2(y2 + y4) + y6)
A = (Δx/3)[y0 + 4(y1 + y3 + y5) + 2(y2 + y4) + y6)]
(FIRST + 4(sum of ODDs)+ 2(sum of EVENs) + LAST)
By creating more and more segments, and adding the areas as
we go along, we would obtain Simpson's Rule :
A = (Δx/3)[y0 + 4(y1 + y3 + y5 + ... + yn-1) + 2(y2 + y4 + ...
+ yn-2) + yn)
]
or
A = (Δx/3)[y0 + 4y1 + 2y2 + 4y3 + 2y4 + 4y5 + 2y6 + ...
+ 4yn-1 + yn ]

code:
Given a and b;
Choose n;
Δx = (b - a)/n ;
xk = a + k Δx, so x0 = a and xn = b ;
k from 1 to n - 1 ;
yk = f(xk) ;
S = f(a) + f(b);
for (k = 1, k ≤ n - 1, k++) {
g = 3 - pow(- 1, k);
S = S + g*f(xk);
}
echo Simpson's area = S;
|
|