Courbes
paramétrées
En coordonnées
cartésiennes
Exemples
En coordonnées
polaires
Exemples
© The scientific sentence. 2010

|
Mathématiques :
Courbes planes paramétrées
Généralités
Définition 1.
Soit I un intervalle de 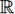 et E2 un plan vectoriel. et E2 un plan vectoriel.
Une appliation vetorielle est une appliation
 : I : I  E2 ,
à valeurs dans le plan vetoriel. E2 ,
à valeurs dans le plan vetoriel.
Si on se placee dans le repère (O, 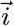 , ,
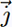 ) , on peut érire : ) , on peut érire :
 (t) = x(t) (t) = x(t)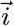 +
y(t) +
y(t)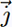 . .
où x : I  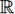 et y : I et y : I 
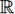 sont deux fontions donnant les coordonnées du vecteur
sont deux fontions donnant les coordonnées du vecteur  (t)
dans la base ( (t)
dans la base (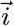 , ,
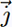 ) . ) .
On identife à l'application  l'application
ƒ de I dans l'application
ƒ de I dans 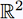 définie par par :
définie par par :
ƒ(t) = (x(t), y(t))
Dans ce chappitre, on étudiera les
fonctions réelles ƒ(t)
à valeur dans 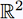 . .
Définition 2.
Soit f : I 
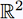 une application vetorielle. une application vetorielle.
• ƒ est continue si et seulement si les fontions
x et y sont continues.
• ƒ est dérivable si et seulement si les fonctions x et y
sont dérivables, et dans ce
cas, on a :
ƒ'(t) = (x'(t), y'(t))
Définition 3.
ƒ est de classe Ck
sur I si f est k fois dérivable sur I , et si les dérivées
sucessives de f sont continues sur I .
Définition 4.
On note:
< , ,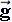 >
le produit scalaire >
le produit scalaire
 . .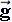
Soit  : I : I 
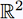 et et
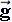 : I : I 
 deux applications vetorielles
de classe C1 sur I . deux applications vetorielles
de classe C1 sur I .
Alors les fonctions :
a) < , ,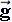 > :
t > :
t  <
< (t), (t),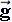 (t)> (t)>
b) 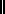  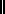 :
t :
t 
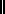  (t) (t)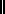 et et
c) det ( , ,
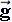 ) : t ) : t  det (
det ( (t), (t),
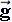 (t)) (t))
sont aussi de classe C1 sur I .
Nous avons:
• <  , ,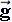 >' =
< >' =
<  ', ',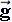 > +
< > +
<  , , 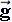 ' > ' >
• 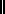  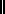 ' =
< ' =
<  ', ', > / > /
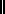  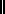
si  ≠ ≠ 
•
det ( , ,
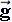 )' =
det ( )' =
det ( ', ', 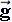 ) +
det ( ) +
det ( , , 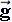 ') ')
Pour démontrer ces relations,
il suffit de formuler leur produit scalaire.
Définition 5.
On appelle arc paramétré de
lasse Ck
toute application f :
 :
I :
I  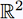
t  ƒ(t) = ƒ(t) = 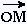 (t) =
(x(t),y(t)) (t) =
(x(t),y(t))
où f est de classe Ck .
L'ensemble Γ = {M(t)= (x(t),y(t)), t
 I} I}
est appelé courbe paramétrée.
On note également Γ :
x = x(t)
y = y(t)
t I I
Définition 6.
Soit f :
 :
I :
I  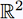
t  ƒ(t) = ƒ(t) = 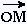 (t) =
(x(t),y(t)) (t) =
(x(t),y(t))
un arc paramétré de
clase C1 .
On appelle point régulier de la
courbe paramétrée γ : "
x = x(t)
y = y(t)
t I, I,
tout point Mo(to) de Γ tel que ƒ'(to) ≠ (0,0).
Si tous les points de la
courbe sont réguliers, celle ci
est dite régulière.
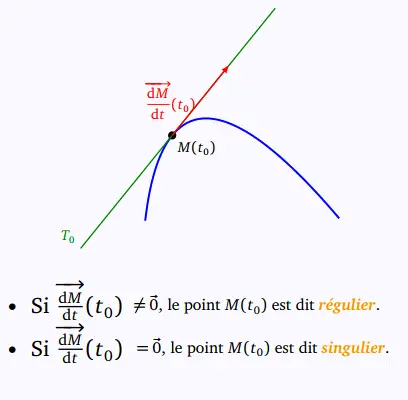
Le vecteur limite ƒ'(to) = (x'(to), y'(to))
est un vecteur tangent à Γ en M(to).
Définition 7.
Si ƒ'(to) = (0,0), alors le point M(to) est dit
stationnaire ou singulier.
|
|