Kirchhoff's rules

An electric circuit contains ordinarily batteries (or other sources), resistors, inductors, and capacitors of known values. To determine the current crossing the circuit elements, we use Kirchhoff's rules referred as the loop rule and the junction rule.

1. The loop rule

The loop rule is a statement of conservation of energy within the circuit because the electric potential is directly related to the potential energy of the carriers. This rule states:

The sum of the potential differences encountered in a complete round-trip around any closed loop in a circuit is zero.

That is: ΣV_i = 0.

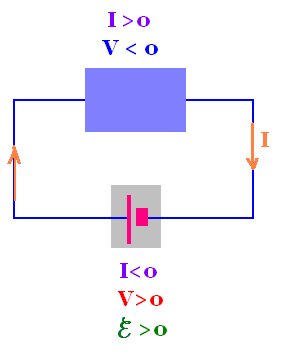
Before using the loop rule, we define the sign convention for the current along the circuit:

The current I is positive when its sense corresponds to the direction og motion of positive charge carriers.

The current is positive
for positive carriers.

2. Examples

2.1. Example 1

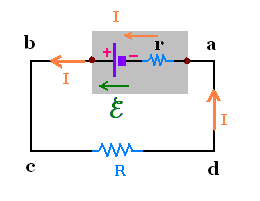
Choosing the counterclockwise sense, we have:

V_b - V_a = ℰ - r I
V_c - V_b = 0
V_d - V_c = - R I
V_a - V_d = 0


ΣV_i = 0

(ℰ - r I) + 0 + ( - R I) + 0 = 0

Solving for I, we find:

I = ℰ /(r + R)

Now, if we chose the clockwise sense, we get:

The potential across the battery decreases: V_a < V_b so ΔV < 0, and the current I is < 0. Hence the potential difference across r is > 0 . Therefore

V_a - V_b = - ℰ + r I
Continuing to traverse the loop, we have:
V_b - V_c = 0
V_c - V_d = + R I
V_d - V_a = 0


The loop rule gives:

- ℰ + r I + R I = 0. That is

I = ℰ /(r + R)

Which is the same result as before.

The result is independent of which way we go around the loop.

2.2. Example 2

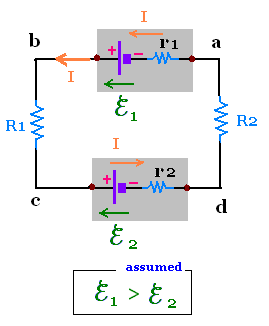
V_b - V_a = ℰ₁ - r₁ I
V_c - V_b = - R₁ I
V_d - V_c = - ℰ₂ - r₂ I
V_a - V_d = - R₂ I

ΣV_i = 0

ℰ₁ - r₁ I - R₁ I - ℰ₂ - r₂ I - R₂ I = 0

ℰ₁ - ℰ₂ = r₁ I + R₁ I - r₂ I + R₂ I

I = (ℰ₁ - ℰ₂)/( r₁ + R₁ + r₂ + R₂)



If ℰ₁ > ℰ₂ then I has a positive value, and the sense of the current is counterclockwise as we assumed before writing the loop rule.

If ℰ₁ < ℰ₂ then I has a negative value, and the sense of the current is clockwise opposite our assumed sense.

Generally, the rule is: If we assume a particular sense for the current at the outset of a problem, and the value of the current turns out to be negative, then this means that the actual sense of the current is opposite the assumed sense.

In more complex circuits, we often cannot predict the sense of the current with certainty at the outset of the analysis. It is the equation solved for the current that tells us automatically its sense in the circuit.

3. The point rule or junction rule

The point rule is a statement that comes from the conservation of charge since charge does not accumulate at any point along the connecting wires. It states that the sum of the currents at a junction is zero:

ΣI_i = 0

In other way The sum of the currents toward a branch point is equal to the sum of the currents away from the same branch point.

ΣI_toward = ΣI_away

3.1. Example 1: Two loops

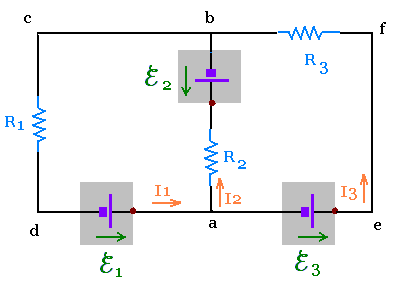
We assume the sense of the currents I₁ and I₃ are counterclockwise and for I₂ clockwise. The equations of the currents will tell us whether these choices are true or wrong. If these assumptions turn out to be wrong, just change the sign of the related current to obtain the actual current, the magnitudes of the currents remain the same.

For simplicity, we include the internal resistance of each battery in the resistance that is in series with that battery.

Loop dabc:

ℰ₁ - R₂ I₂ - ℰ₂ - R₁ I₁ = 0

Loop aefb:

ℰ₃ - R₃ I₃ + ℰ₂ + R₂ I₂ = 0

Loop defc:

ℰ₁ + ℰ₃ - R₃ I₃ - R₁ I₁ = 0

We have three unknowns I₁, I₂, and I₃. On of these equations is irrelevant because it is obtained from two others. Hence we keep just two of them: the first and the third equations.

Point a:

I₁ = I₂ + I₃

Substituting this value in the first equation (loop dabc), we obtain:

ℰ₁ - ℰ₂ = R₁ I₁ + R₂ I₂ =
R₁ (I₂ + I₃) + R₂ I₂ =
(R₁ + R₂)I₂ + R₁ I₃)

Finally, we have the two equations:

ℰ₁ - ℰ₂ = (R₁ + R₂)I₂ + R₁ I₃)    (Eq. 1)
ℰ₁ + ℰ₃ = R₃ I₃ + R₁ I₁    (Eq. 2)

Substituting one in the other, we find:

I₂ = [ℰ₁ - (R1/R3)ℰ₃ - (1 + R1/R3)ℰ₂]/[R₁ + R₂ + (R₁ R₂/R₃)]

Using the equation (Eq. 1) , we find I₃, and the equation of the point a , we find I₁.

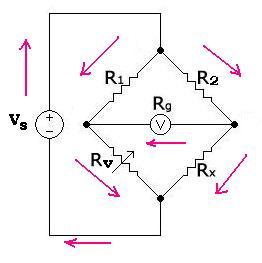
3.2. Example 2:Electrical Bridges

3.2.1. Wheatstone bridge:

The Wheatstone bridge is used to measure an unknown resistance.

In this figure, Rx is the unknown value of a resistance to be measured, and Rv is a variable resistor. The idea is to vary the resistance Rv until the galvanometer (resistance Rg and voltage Vg) indicates zero.
Once this condition is achieved, we can find the value of Rx. Indeed:
We have:

Ig + I1 = Iv
Ig + Ix = I2
R2 I2 + Rg Ig - R1 I1 = 0
Rv Iv - Rx Ix + Rg Ig = 0


Ig = 0 implies:
I1 = Iv
Ix = I2
R2 I2 = R1 I1
RvIv = Rx Ix
Then:
Rx = Rv Iv / Ix = Rv I1/I2 = Rv R2/R1

Rx/Rv = R2/R1    (1)

We can also express the value of the voltage Vg depending on the value of the voltage source Vs:

Vs = R1I1 + Rv (I1 + Ig) → I1 = (Vs - RvIg)/(R1 + Rv)    (a)
Vs = R2I2 + Rx (I2 - Ig) → I2 = (Vs + RxIg)/(R2 + Rx)    (b)
We have:
Vg = R1I1 - R2I2

With the equations (a) and (b), we obtain:
Vg = Vs(R1/(R1 + Rv)) - Vs(R2/(R2 + Rx)) - Ig[R1Rv/(R1 + Rv) + R2Rx/(R2 + Rx)]
As Ig is very small, then the term if Ig is negligible, we have finally:


Vg = [R1/(R1 + Rv)- R2/(R2 + Rx)]Vs




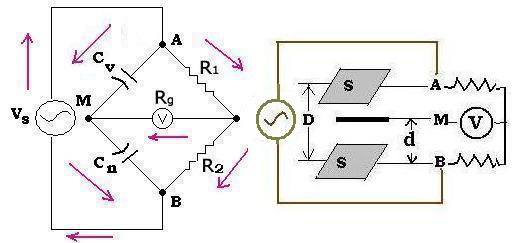
3.2.2. Modified Wheatstone bridge: Sauty Bridge:

It is used to measure a level or pressure of a liquid in a container. It contains two capacitors and two resistors.
We have the same reasoning as for the Wheatstone bridge. Since the current is alternating, the expressions of the currents and voltages are effective quantities. The impedance of a capacitor is Z = 1/Cω (ω is the frequency of the alternating current), as in the relationship (1), we have:
R2 / Cω = R1/Cn or

Cn/Cv = R1/R2    (2)


The expressions of the two capacitors are:
Cn = ε₀ ε_r S / d
Cv = ε₀ ε_r S / (D - d)
Then:
Cv/Cn = d/(D - d) = (d - 1)/D

The distance "d" is fixed and known, so is the value of Cn. If the distances "D" changes; then the distance "D - d" between A and M changes; that gives a new value of Cv; according to the value of Cn.

The expression, as for the Wheatstone bridge, of the voltage V takes the expression:

V = [Cn/(Cv + Cn) - R1/(R1 + R2)]Vs

We can write:
V = [1/(Cv /Cn + 1) - R1/(R1 + R2)]Vs = [(D - d)/D - R1/(R1 + R2)]Vs

V = [(1 - d/D) - R1/(R1 + R2)]Vs

For each displacement "D - d" or "D", we have directly a value measured in the galvanometer V. This is the principle of a flow transmitter of a fluid.



Application:

D = 10 cm , d = 4 cm, R1 = R2 = R3 = 5 kΩ, Vs = 110 Volts
V/Vs = (10 - 4)/10 - 5/(5 + 5) = 0.6 -0.5
V = Vs/10 = 110/10 = 11 Volts
For a distance of 6 cm, we get 11 Volts in the galvanometer.