1. definitions

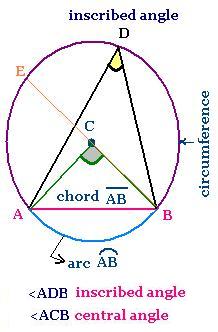
The inscribed angle <ADB and the central angle <ACB intercept the same arc AB.
We have CA = CB = radius of the cercle of center C which is equal to the half of the diameter BE.
The circumference measures 2π x radius = π x diameter.

A sector is the area delimited by two radii and an arc lying between these two radii, is. A segment is the area delimited by a chord and an arc.

How to define a radian?

By definition, one radian is the measure of a unit plane angle, equal to the central angle of a circle intercepting an arc equal in length to the radius.

The circumference "C" of a circle of radius "R" measures 2πR. We have then 2πR/R = 2π = 8.28 arcs meausuring R in the circumference 2πR.

If 180 degrees corresponds to π radian, one radian = 180/π = 57.29 degrees. We write 1 rad = 57.29^o.

The rad is used under the SI (Systeme International d'Unites) unit.

2. Inscribed angles

CD = CB, because both are radii of the cercle. Then <BCD is an isosceles triange. The angle <B2 and <D are then equals. <B2 = <D.

We can write:
(180 - <C) + <B2 + <D = 180
Then:
<D = <C/2

An inscribed angle is the half of the central angle, when they both intercept the same arc.

Draw the chord DP that passes by the center of the circle "C"; we have:
Angle <D = <ADB = <ADP + <BDP = <ACP/2 + <BCP/2 = <ACB/2. Then
<D = <C/2
An inscribed angle is the half of the central angle, when they both intercept the same arc.

Draw the diameter DP, we have:
Angle <D = <ADB = <ADP - <BDP = <ACP/2 - <BCP/2 = <ACB/2 <C/2
Then:
<D = <C/2
An inscribed angle is the half of the central angle, when they both intercept the same arc.

Draw a parallel BP to DA; we have:
Angle <D = Angle <B.
The angle <B is an inscribed angle that intercepts the arc PD which is equal to to the arc BD (because AD and BP are parallel).
Then:
<D = <C/2

An inscribed angle is the half of the central angle, when they both intercept the same arc; even in the limit case where the inscribed angle is formed by a tangent and a chord.

3. Two intersecting chords:

Draw two chords AC and DB in the circle; we have:
Angle <APB + Angle <BPC = 180
<BPC = 180 - (<CBP + <PCB) = 180 - (arc DC/2 + arc AB)
Then:
<APB = 180 - <BPC = 180 - 180 + arc DC/2 + arc AB/2

<APB = (arc DC+ arc AB)/2

<APB = (arc DC + arc AB)/2

4. Angle of two secants:

Draw two secants BC and EC; we have:
Angle <EAB = Angle <BDE = Arc BE /2. Then:
<BDC = <EAC
<C + <B1 + <B2 + <E1 + <E2 = 180
<C + <B1 + <E1 + <B2 + <E2 = 180
<C + arc AD/2 + arc AD/2 = 180 - (<E2 + <B2)
We have:
<E2 + <B2 = arc ED/2 + arc AB/2
And, for the whole circumference:
(arc AB + arc BE + arc ED + arc DA)/2 = 180
Then:
<C = (arc AB + arc BE + arc ED + arc DA)/2 - arc AD - arc ED/2 - arc AB/2

<C = arc BE/2 - arc AD/2

<C = (arc BE - arc AD)/2

5. Two tangents:

Draw two tangents AO and BO; we have:
Angle <BAO = minor arc AB/2 = <ABO
<BAO + <ABO = 2 <BAO = 180 - minor arc AB.
We have for the whole circumference:
180 = (major arc AB + minor arc AB)/2
Then:
<AOB = 180 - 2 <BAO = (major arc AB + minor arc AB)/2 - minor AB = (major arc AB - minor arc AB)/2

<AOB = (major AB - minor AB)/2

6. Tangent and secant :

Draw a secants BC and a tangent AC; we have:
Angle <A = Arc AD /2. Then:
<C + <A = <D = arc AB/2. So <C = arc AB/2 - <A = arc AB/2 - arc AD/2
<C = (arc AB - arc AD)/2

<C = (arc AB - arc AD)/2

7. Two secants

The two angles PAB and PBA intercept the same arc AB/2 (they are formed by the chord AB and a tangent). Then, the triangle PAB is isosceles. Furthermore PA = PB.

The two segments drawn from an exterior point of a circle and tangent to this circle are equal in length.

According to the sine law, if two angles of a triangle are congruent, their opposite sizes are also congruent, then the triangle is isosceles.
AP/sinB = PB/sinA. If angle A = angle B, then AP = BP, and the triangle APB is isosceles.