Mathématiques 2: Valeur absolue

1. Définition

La valeur absolue  ou le module  
d'un nombre réel est égale à ce nombre réel lui 
même quand il est positif; et est égale à son 
opposé lorsque ce nombre est négatif. 

La valeur absolue d'un nombre x est notée |x|. 

Si |x| est la valeur absolue d'un nombre réel, 
alors 

         x si x ≥ 0
|x| = 
       - x si x < 0 

2. Exemples:

|+ 3| = 3 
|- 2| = - (-2) = 2 
|0| = 0 
|1/8| = 1/8 

3. Propriétés:

∀a ∈ ℝ : 
|a| ≥ 0
|a| = |- a| 
a ≤ |a| 
- a ≤ |a|

∀a, b ∈ ℝ : 
|a + b| ≤ |a| + |b|
|a| - |b| ≤ |a - b| 
|a . b| = |a| . |b|
|a / b| = |a| / |b| si b ≠ 0
|a| = |b| ↔ a = b ou a = - b 

∀r > 0 : |a| ≤ r ↔ - r ≤ a ≤ r 
∀r > 0 : |a| ≥ r ↔ a ≤ - r ou a ≥ r 
∀r > 0 : |a - b| ≤ r ↔ (b - r) ≤ a ≤ (b + r)

4. Valeur absolue, équations et inéquations:

Afin d'utiliser la définition d'une valeur 
absolue et ses propriétés, nous allons 
résoudre dans R les équations et inéquations 
suivantes:


1) |x + 1| = 2x - 3 
2) |x2 - 1| = |x + 5| 
3) - 1 ≤ (3x + 1)/(x + 2) ≤ 1 
4) |2x + 3| - |3x - 2| ≤ 0.
5) 1 ≤ |2x + 1| < 3 
6) x2 + 3x + 2 ≥ |x + 1| 
7)|x2 + 3x + 2| ≤ x - 1



1) Par définition |x + 1| = 
x + 1 si x + 1 ≥ 0
- (x + 1) si x + 1 <  0

Donc  |x + 1| =
x + 1 si x ≥ - 1
- x - 1 si x < - 1

Ainsi,
si x ≥ - 1, l'équation s'écrit x + 1 = 2x - 3 , x = 4
si x < - 1, l'équation s'écrit - x - 1 = 2x - 3 , 3x = 2, 
x = 2/3, solution à rejeter puisque x < - 1.

Donc l'équation a pour unique solution 4.



2) |x2 - 1| = |x + 5| 

Si deux réels sont égaux en valeur absolue alors ils 
sont égaux ou opposées. L'équation donnée
est donc équivalente à: 
x2 - 1 = x + 5 ou x2 - 1 = - x -  5 , x2 - x - 6 = 0 ou 
x2 + x + 4 = 0:
L'équation 
x2 - x - 6 = 0 , (x - 3)(x+2) = 0 a pour solutions 
- 2 et 3. Par contre, 
l'équation x2 + x + 4 = 0 n'a pas de solution réelle puisque 
Δ = 1  -  16 =  - 15 < 0. Les solutions de l'équation 
donnée sont donc - 2 et 3




3) - 1 ≤ (3x + 1)/(x + 2) ≤ 1 

3) Cette inéquation n'est définie que si x ≠ 2. 
Elle s'écrit de façon équivalente sous la forme
|(3x + 1)/(x + 2)| ≤ 1. 

Comme |a / b| = |a| / |b| si b ≠ 0

et |b| > 0, l'inéquation ci-dessus est équivalente à 
|(3x + 1) ≤ (x + 2)

Vu que |(3x + 1) et (x + 2)| sont positifs, on a 

(3x + 1)2 ≤ (x + 2)2

(3x + 1)2 - (x + 2)2  ≤ 0

[(3x + 1) - (x + 2)][(3x + 1) + (x + 2)] 

(4x + 3)(2x - 1) ≤ 0. 

Le premier membre s'annule pour x = - 3/14 ou x = 1/2 
le trinôme est négatifpour les valeurs de x 
comprises entre -3/4 et 1/2. L'ensemble des solutions 
est [- 3/4, +1/2].



4)
|2x + 3| - |3x - 2| ≤ 0.

Soit h(x) = |2x + 3| - |3x - 2|

Le premier terme de h possède une racine 
en x = - 3 et le deuxième possède une racine 
en x = 2 . 

Tableau de signes: 


 
      
-∞ < x≤ -3/2
   
 -3/2 ≤ x ≤ 2/3 
  
 x ≥ 2/3
  
 
 |2x + 3|
   
 -2x - 3 
   
  2x + 3 
   
2x + 3 
  
 
 |3x - 2|
   
 -3x + 2 
   
-3x + 2  
   
 3x - 2 
  
 
 h(x)
   
x - 5  
   
 5x + 1 
   
- x + 5 
  


La fonction h est donc définie comme suit:

     x - 5 si x  ≤  -3/2
h(x) = 5x + 1 si - 3/2  ≤  x  ≤  2/3
     -x + 5 si x  ≥  2/3.

Examinons maintenant le signe de h sur chaque 
intervalle :

h(x) = x - 5  ≤  0 si x  ≤  5, 
donc sur ] - ∞ , -3/2] on a h(x)  ≤  0.

h(x) = 5x + 1  ≤  0 si x  ≤  -1/5, 
donc h(x)  ≤  0 sur [-3/2, -1/5] et 
h(x)  ≥  0 sur [-1/5, 2/3]

h(x) = - x + 5  ≤  0 si x  ≥  5, 
donc h(x)  ≤  0 sur  [5,∞ [ et 
h(x) ≥  0 sur [2/3, 5].


Ainsi la solution à l'inéquation 
est ]- ∞ , -1/5] ∪ [5,∞ [.



5)
L'inéquation 1 ≤ |2x + 1| < 3  est équivalente 
au systµeme

1 ≤ |2x + 1|     (1)
|2x + 1| ≤ 3     (2)

L'inéquation (1) peut s'écrire 
2x + 1 ≤ - 1 ou 2x + 1 ≥ 1 ↔  x ≤ - 1 ou x ≥ 0
Son ensemble de solutions est:
S1 = ] - ∞, - 1]∪ [0; +∞[.

L'inéquation (2) peut s'écrire 
- 3 ≤ 2x + 1 ≤ 3 , - 4  ≤ 2x ≤ 2 ↔  - 2 ≤ x ≤ 1 
Son ensemble de solutions est:
S2 = ]- 2, 1[.

Les inéquations (1) et (2) doivent être vériées 
simultanément. Par conséquent, les solutions doivent 
être communes aux deux inéquations. L'ensemble de 
solutions est donc l'intersection des ensembles 
S1 et S2. Donc S = S1 ∩ S2 = ]- 2; - 1] ∪ [0; 1[.



6) x2 + 3x + 2 ≥ |x + 1| 

Si x ≥ - 1, l'inéquation s'écrit
x2 + 3x + 2  ≥ x + 1,  x2 + 2x + 1 ≥ 0, 
(x + 1)2 ≥ 0. Le carrée d'un
réel étant toujours positif, toute valeur de x est 
solution avec la condition x ≥ - 1. Ainsi l'ensemble
des solutions est S1 = [- 1; + ∞[.

Si x < - 1, l'inéquation s'écrit 
x2 + 3x + 2 ≥ - x - 1 , x2 + 4x + 3 ≥ 0, (x + 1)(x + 3) ≥ 0 
Son ensemble de solutions est S2 = ] - ∞, - 3] ∪ {- 1} 
puisque la condition est x < - 1.

Ainsi l'ensemble S des solutions de l'inéquation 
donnée est la réunion des ensembles S1 et S2.
S = S1 ∪S2 = ] - ∞, - 3] ∪ [- 1; + ∞[.




7)|x2 + 3x + 2| ≤ x - 1

Les zéros du trinôme x2 + 3 x + 2 = (x + 1)(x + 2) 
sont  - 1 et  - 2. De plus, comme le coefficient de 
x2 est positif, ce trinôme est positif pour les 
valeurs de x inférieures à - 2 ou supérieures à - 1 
et négatif pour celles comprises entre - 2 et - 1. 

Donc |x2 + 3x + 2| = 
x2 + 3x + 2 si x ≤ - 2 ou x ≥ - 1
- x2  - 3x  - 2 si  - 2 ≤  x ≤   - 1

x ≤ - 2 ou x ≥ - 1, l'inéquation s'écrit 
x2 + 3x + 2 ≤ x - 1 , x2 + 2x + 3 ≤ 0, 
Cette inéquation n'admet aucune solution puisque 
le discriminant Δ = 4  - 12 =  - 8 < 0.

Si - 2 ≤ x ≤ - 1, l'inéquation s'écrit  
- x22 - 3x - 2 ≤  x - 1, x2 + 4x + 1 ≥ 0. 
Le discriminant Δ =  16 - 4 = 12, les
zéros du trinôme sont x1 = - (4 + 2√3)/2 
= - (2 + √3) = - 3.7 
et x2 = - (4 - 2√3)/2 = - (2 - √3) = - 0.3.

Ce trinôme est positif si x ≤ x1 ou x > x2. 
Ces valeurs ne satisfont pas la condition - 2 ≤ x ≤ - 1, 
c'est à dire les valeurs de x1 = - 3.7 et x2 = - 0.3 ne 
se trouvent pas dans - 2 ≤ x ≤ - 1 ou [- 2, -1].
Donc l'ensemble des solutions de cette deuxième 
inégalité est également vide.

Finalement, l'inéquation donnée n'est vérifée pour 
aucune valeur de x: son ensemble de solutions est
l'ensemble vide Φ.




8) h(x) = |7 x - 2|- |3 x - 3| ≥ 2

|7 x - 2| = 
7 x - 2 si 7 x - 2 ≥ 0, x ≥ 2/7
- 7 x + 2 si 7 x - 2  < 0,  x < 2/7

|3 x - 3| = 
3 x - 3 si 3 x - 3  ≥ 0, x ≥ 1
- 7 x + 2 si 3 x - 3  < 0,  x < 1



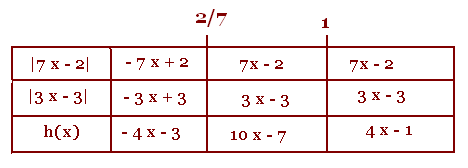- 4x - 3 ≥ 0 x ≤ - 3/4,  dans ]- ∞, 2/7] 
Donc S1 = ]- ∞, - 3/4] 

10 x - 7 ≥ 0 x ≥ 7/10 dans [2/7, 1]
Donc S2 = [7/10, 1]

4 x - 1 ≥ 0 x ≥ 1/4,  dans [1, + ∞[
Donc S3 = [1/4, + ∞[

S =   ]- ∞, - 3/4] ∪ [7/10, 1] ∪ [1/4, + ∞[.




9) Soit l'équation suivante: 

|- 5 x + 3| - 5 =  √(4 x + 5)

Il faut que (4 x + 5) soit positif ou null, 
c'est à dire x ≥ - 5/4.

|- 5 x + 3| =  √(4 x + 5)  +  5

a) - 5 x + 3  ≥ 0, x ≤ 3/5
- 5 x + 3 =  √(4 x + 5)  +  5
- 5 x - 2 =  √(4 x + 5) 
(- 5 x - 2)2 =  4 x + 5 
25 x2 + 20 x + 4 =  4 x + 5
25 x2 + 16 x - 1 =  0
x1 = 0.06
x2 = - 0.7

b) - 5 x + 3  ≤ 0, x ≥ 3/5
5 x - 3 =  √(4 x + 5)  +  5
5 x - 8 =  √(4 x + 5)  
(5 x - 8)2 =  (4 x + 5) 
25 x2 - 80 x + 64 =  4 x + 5
25 x2 - 84 x + 59 = 0
Pas de solutions.

Avec la contrainte x ≤ 3/5 = 0.6 
x1 = 0.06 et x2 = - 0.7 correspondent bien aux 
solutions. Avec la contarinte de départ 
x ≥ - 5/4 = - 1.25, x1 = 0.06 et x2 = - 0.7 
restent des solutons. Ainsi, l'ensemble des solutions 
de l'équation donnée est:

S = {0.06 et x2 = - 0.7}