Mathématiques 45: Probabilités
Formule de Bayes

1. Thomas Bayes

Thomas Bayes est un mathématicien britannique. Il est né en 1702 à Londres et mort en 1761 à Tunbridge Wells au Royaume Uni. Prononcer baiz (en Français) ou Beiz (in English).

Les travaux de Bayes sur les probablités ont été étendus pa Laplace.


En théorie des probabilités, le théorème de Bayes utilise les probabilités conditionnelles. Il permet, étant donné deux événements A et B, de déterminer la probabilité de B sachant A, si l’on connaît les probabilités de , de B, et de A sachant B.

Cette formule s'ecrit:

P(A|B) x P(B) = P(A∩B) = P(B|A) x P(A)

2. Exemple

On reconsidère trois boîtes différentes:

La première #1 contient 3 crayons H et 2 crayons B,
La deuxière #2 contient 6 crayons H et 4 crayons B,
La troisième #3 contient 2 crayons H et 3 crayons B.

Nous avons calculé la probabilité totale de l'événement «choisir un crayon de type B» après avoir choisi une boîte au hasard.

Maintenant, nous allons plutôt calculer la probabilité de l'événement «choisir une boîte de type A1» (A2, ou A3) après avoir choisi un crayon de type B.

Autrement dit, nous réponderons à la question :

Supposons que le crayon choisi soit de type B; quelle est la probabilité que ce crayon provienne de la boîte #1 (ou #2 ou #3)?

Voici les événements:

A1: choisir la boîte #1
A2: choisir la boîte #2
A3: choisir la boîte #3

B: choisir un crayon de type B



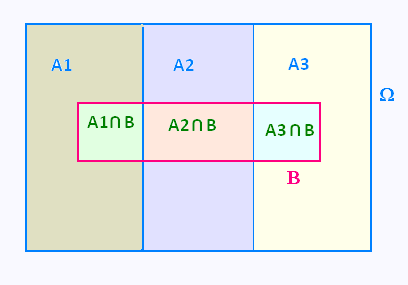
Les trois boites constituent ensemble l'univers des probabilités Ω. Ainsi les 3 évenements A1, A2, et A3 sont incompatibles et leur union donne Ω.

Les intersections A1∩B, A2∩B, et A3∩B sont aussi disjointes et leur union donne B.

B = (A1∩B) ∪ (A2∩B) ∪ (A3∩B) .

En premier lieu, on coisi une boîte, donc tomber sur un crayon B peut se produire dans la boîte #1, dans la boîte #2, ou dans la boîte #3,



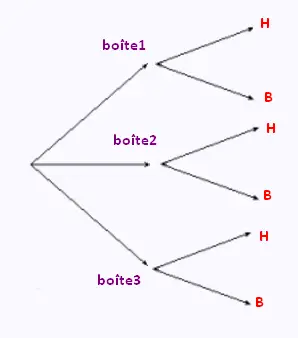
L'événement B peut se produire de trois manières différentes:

• Si on choisit la boîte #1, la probabilié de tomber sur un crayon B est
p1(B) = p(B∩A1) = p(A1) x p(B|A1) = = p(A1∩B) = p(B) x p(A1|B).
D'où:

p(A1|B) = p(A1) x p(B|A1)/p(B)

• Si on choisit la boîte #2, la probabilié de tomber sur un crayon B est
p2(B) = p(B∩A2) = p(A2) x p(B|A2) = = p(A2∩B) = p(B) x p(A2|B).
D'où:

p(A2|B) = p(A2) x p(B|A2)/p(B)

• Si on choisit la boîte #3, la probabilié de tomber sur un crayon B est
p3(B) = p(B∩A3) = p(A3) x p(B|A3) = = p(A3∩B) = p(B) x p(A3|B).
D'où:

p(A3|B) = p(A3) x p(B|A3)/p(B)

La probabilité totale de B est :

p(B) = p1(B) + p2(B) + p3(B) = p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3)

p(B) = p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3)

p(A1|B) = p(A1) x p(B|A1)/(p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3))

p(A2|B) = p(A2) x p(B|A2)/(p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3))

p(A3|B) = p(A3) x p(B|A3)/(p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3))

Nous avons donc pour notre exemple:

p(A1) x p(B|A1) = (1/3) x (2/5)
p(B) = (1/3) x (2/5) + (1/3) x (4/10) + (1/3) x (3/5) = 7/15

Donc:

p(A1|B) = (1/3) x (2/5)/ 7/15 = 2/7

De même:

p(A2|B) = (1/3) x (4/10) / 7/15 = 2/7, et
p(A3|B) = (1/3) x (3/5)/ 7/15 = 3/7 .

Sur un arbre de probabilités, on aura:

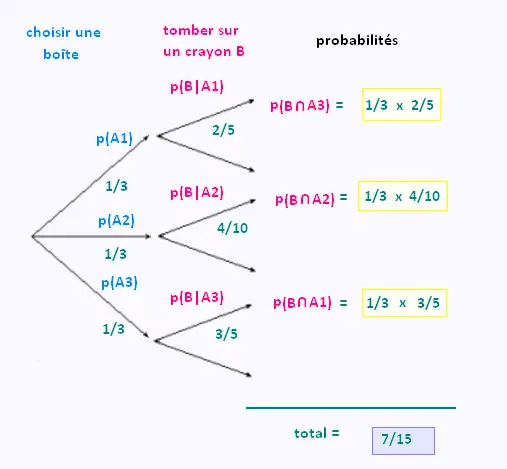
3. Formule de Bayes

On généralise pour une partition de n événements.

Pour une partition de n événements: A₁, A₂, A₃, ...A_n, de probabilités non nulle, d'un ensemble fondamental Ω associé à une expérience aléatoire, la probabilité conditionnelle p(A_r|B) de l'un de ces événements attaché à un évenement quelconque B associé à cette expérience aléatoire est:

p(A_r|B) = p(A_r) x p(B|A_r)/ Σ(p(A_i) x p(B|A_i)
i = 1 → n

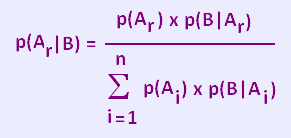
4. Autre exemple

On cosidère 3 groupes d'élèves en musique G1, G2 et G3.

Le groupe G1 compte 10 élèves dont 3 pratiquent l'accordéon,
Le groupe G2 compte 20 élèves dont 4 pratiquent l'accordéon,
Le groupe G3 compte 30 élèves dont 3 pratiquent l'accordéon,

On choisit un élève au hasard et on constate qu'il pratique l'accordéon. Quelle est la probabilité qu'il provienne du groupe G2?

Voici les événements:

A1: L'élève provient du groupe G1
A2: L'élève provient du groupe G2
A3: L'élève provient du groupe G3

B: L'élève pratique l'accordéon

Nous avons:

Probabilité de provenir de G2: p(A2) = 20/60 = 1/3

Probabilité de pratiquer l'accordéon sachant que la provenance est G2: p(B|A2) = 4/20 = 1/5

Probabilité de pratiquer l'accordéon ET de provenir du groupe G2: p(B∩A2) = p(A2) x p(B|A2) = 1/3 x 1/5 = 1/15

Probabilité totale: p(B) = 1/6 x 3/10 + 1/3 x 1/5 + 1/2 x 1/10 = 1/20 + 1/15 + 1/20 = 1/6

D'où, selon la formule Bayes:

p(A2|B) = p(A2) x p(B|A2)/ p(B) = (1/15)/(1/6) = 2/5

Sachant qu'un élève pratique l'accordéon, la probabilité qu'il provienne du groupe G2 est de 40%.