Mathématiques
2
Probabilités
Probabilités conditionnelles
Exercices divers
© The scientific sentence. 2010
|
probabilités totales
Mathématiques 45: Probabilités
Probabilités totales
1. Exemple

On considère trois boîtes différentes:
La première #1 contient 3 crayons H et 2 crayons B,
La deuxière #2 contient 6 crayons H et 4 crayons B,
La troisième #3 contient 2 crayons H et 3 crayons B.
Si on choisie une boîte au hasard, puis un crayon au hasard
dans cette boîte, quelle est la probabilité que l'on tire un crayon
de type B?
Voici les événements:
A1: choisir la boîte #1
A2: choisir la boîte #2
A3: choisir la boîte #3
B: choisir un crayon de type B
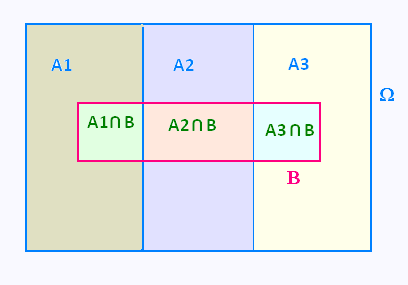
Les trois boites constituent ensemble l'univers des probabilités
Ω. Ainsi les 3 évenements A1, A2, et A3 sont incompatibles
et leur union donne Ω.
Les intersections B∩A1, B∩A2, et B∩A3 sont aussi disjointes et
leur union donne B.
B = (B∩A1) ∪ (B∩A2) ∪ (B∩A3) .
En premier lieu, on coisi une boîte, donc tomber sur un crayon B peut
se produire dans la boîte #1, dans la boîte #2, ou dans la boîte #3,
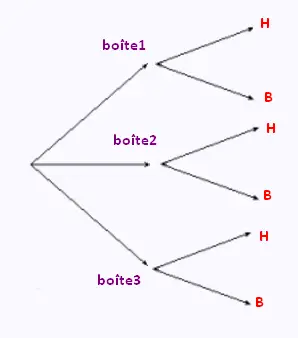
L'événement B peut se produire de trois
manières différentes:
• Si on choisit la boîte #1, la probabilié de tomber sur un crayon B est
p1(B) = p(B∩A1) = p(A1) x p(B|A1).
• Si on choisit la boîte #2, la probabilié de tomber sur un crayon B est
p2(B) = p(B∩A2) = p(A2) x p(B|A2).
• Si on choisit la boîte #3, la probabilié de tomber sur un crayon B est
p3(B) = p(B∩A3) = p(A3) x p(B|A3).
La probabilité totale de B est donc:
p(B) = p1(B) + p2(B) + p3(B) =
p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3)
= (1/3) x (2/5) + (1/3) x (4/10) + (1/3) x (3/5) = 7/15
Sur un arbre de probabilités, on aura:
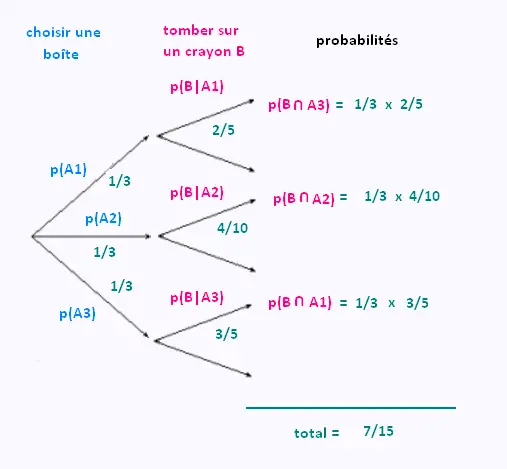
2. Théorène des probabilités totales
On généralise pour une partition de n événements.
Pour une partition de n événements: A1, A2, A3, ...An,
de probabilités non nulle, d'un ensemble fondamental Ω associé à une expérience aléatoire, la
probabilité totale d'un événement quelconque B associé à cette expérience
aléatoire est:
p(B) = p(A1) x p(B|A1) + p(A2) x p(B|A2) + p(A3) x p(B|A3) + ...
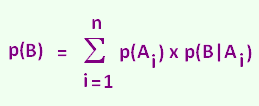
|