Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Angular momentum
1. Angular momentum
A force exerted on an object, that can be translated,
causes its linear velocity to change: F = m a. A torque
exerted on an object, that can be rotated, causes its
angular velocity to change τ = I α. Any object
can rotate about an axis.
Let's recall that a moment(of force) is the tendency
of the force to oscillate or rotate an object; and the
momentumis the quantity of motion of an object.
Linear momentum if the motion of the object
is linear and uniform; and angular momentum when
the motion of the object is circular. The linear momentum is
a vector quantity as the velocity v is; and the angular momentum
is also a vector as ω is. A linear momentum "P" has the same
direction as the linear velocity v . The direction of the angular
momentum "L" is the direction if the angular velocity "ω".
The direction of ω is on the rotation axis. This direction
is perpendicular to the plane from where the angular momentum
stems; that is the plane formed by the position vector and the
linear velocity (then linear momentum) of the object. We remember
that the moment of inertia of an object is relative to an axis;
whereas the torque and the angular momentum are relative to a
reference point. The concept of angular momentum is very
useful in rotational dynamics.
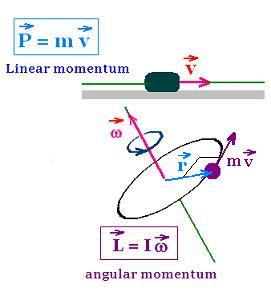
2. Angular momentum of a single particle
The angular momentum "l" of a particle about a referenec point O is
defined as:
l = r x p
where r is the position vectore of the particle measured from O;
and p is its linear momentum. The cross product shows that the
linear momentum is a vector quantity. It is perpendicular to the plane
containing r and p. Its direction is defined by the right-hand rule.
Its dimension is [mass][length2][time -1]; and
its SI unit is kg.m/s. Its magnitude is = mrvsinθ, where
θ is the angle formed by r and p in this order. Recall:
The angular momentum is relative to reference point about
which is defined and then calculated.
The simple case is when a particle travels in a circle of radius r.
The angular momentum is the determined about the center of cercle,
that is here, the point of reference. In circular motion, at each
point of the circle, the velocity v is perpendicular to r,
therefore θ = 90o and the expression of the
angular mmentum takes the following simple form:
l = r x p = r x mv = m r x v = m r v sin θ = mrv
Since v = ω r, we have then:
l = mr r ω = mωr2
If the vectors r and p are contained in the plane xy,
l will point in the z-axis. Its direction depends on the
sense of the rotation. It is given by the right-hand rule.
Viewed from the + z direction, if the motion is counterclockwise,
l is toward + z, hence lz is positive. If the motion
is clockwise, l is toward -z, and lz is negative.
This is exacly the direction of ωz. If k
is the unit vector of the z-axis, we can write:
l = lz k = mωzr2 k
If the motion is also uniform, ωz will be
constant equal to ω arewe will have:
l = lz k = mωr2 k
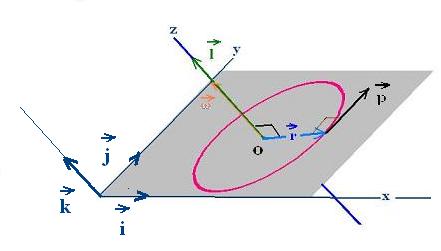
In an inertial frame, the second Newton's law is writen as ΣF = ma, where
ΣF is the net force exerted on the particle of mass m,
and a the produced acceleration. In terms of linear momentum,
this equation is written as: ΣF = dp/dt; that is the
derivative of the linear momentum p of the particle. In
rotational motion, the net force ΣF exerted on a
particle produces a torque a net torque Στ
= r x ΣF, where r is the position vector of the particle
nad ΣF is the net force exerted on the particle.
We want to link this τ to angular momentum l of the particle.
With l = r x p. The time derivative of the angular momentum is:
dl/dt = dr/dt x p + r x dp/dt
The first term der/dt x p =0 because dr/dt = v, and
v x p = m v x v = 0. Therefore:
dl/dt = r x dp/dt = r x ΣF = Στ
We obtain, therefore an important formula:
Στ = dl/dt
The net torque exerted on a particle relative a point is equal
to the time rate of change of its angular momentum relative to that point. The
angular momentum is measured in an inertial frame .
2. Angular momentum of a system of particles
For a system of particles, the total angular momentum L relative to
a reference point is equal to the vector sum of individual angular momenta
li all relative to that same point, that is L = Σli.
The time derivative of L is: dL/dt = Σdli/dt =
Σ(Στi) (sum for all particles, and the
sum of all torques for each particle, that is the sum for all
particles of their net torques). This sum of net torques is equal to:
- The sum of the internal torques on the particles due the forces
they exert on each other within the system, which they cancel in pairs
(according to the Newton's third law: Fij = - Fji
and τij = - τji)
- The sum of external torques.
Therefore, the total net torque is equal to the external net torque.
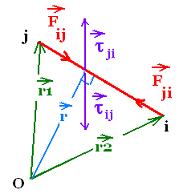
dL/dt = Στext
Only external torques can change the angular momentum
of a system. The torques and the angular momentum are measured
about the same reference point in an inertial frame.
Recall an object rotates about a fixed axis. Its angular velocity
ω and its moment of inertia are referred to an axis; whereas
torque and angular momentum are both relative a refrence point.
3. Angular momentum of a rigid object
We want a relation between the moment of inertia relative
to a fixed axis and the angular momentum of a rigid object
with sufficient symetry relative to a point in this same axis.
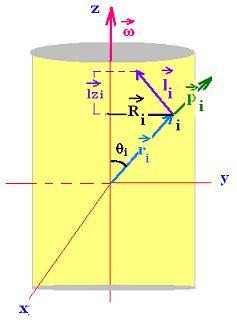
It we choose the z-axis (or axial) about the rigid object rotates,
the component of the angular momentum of the object is Lz =
Σliz. The z-comonent of the angular momentum of the particle i is
li= ri x pi = miviri sin (ri, vi)
ri and pi are perpendicular, so:
li = miviri
Since vi = ωz Ri, and Ri = ri sinθi we have then:
li = miωz Riri
and liz= miωz Ririsinθi = miωz Ri2
li has both an axial and radial component. It doesn't depend
of the location of the origin in the axis. Its expression is valid
for any origin as long as the origin is on the axis.
Therefore:
Lz = Σliz = Σ miωz Ri2 = ωz Σ mi Ri2 = ωz I
Lz = I ωz
Iz is the moment of inertia of the rigid object relative
to the z-axis of rotation.
With an abject that has sufficient symetry, the radial components
within the object cancel, so L is parallel to lz. We have then:
L = I ω
3. Equation of motion for a rigid object
rotating about a fixed axis
Taking the time derivetive of the above
equation giges:
dLz/dt = I dωz/dt = I αz
But dLz/dt = Στext, so
Στext = I αz
This the equation of motion of a rotating rigid object
about a fixed z-axis.
|
|