Rotational dynamics: Atwood's machine
1.Atwood's machine
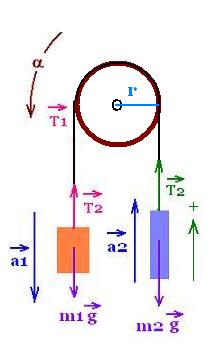
Atwood's machine consists of a frictionless and not
stretching pulley that hangs two masses attached to a string that
does not slip on the pulley, as shown in the figure.
This machine uses Newton�s second law for
translational (F = m a) and rotational (τ = I α) motions .
If m is the mass of the pulley of radius r, its moment
of inertia is I.
The masses m1 and
m2 are pulled by the tensions T1 and T2 respectively.
1.1. Second Newton's law for rotation
The second Newton's law for rotation for the pulley is:
τnet = Στ = I α (1)
That is :
T1 r - T2 r = r(T1 - T2) = I α (1')
α is the angular acceleration of the pulley.
1.2. Second Newton's law for translation
The second Newton's law for translation of the two masses is:
For m1:
m1 g - T1 = m1 a (4)
For m2:
- m2 g + T2 = m2 a (5)
From (4):
T1 = m1 g - m1 a = m1 (g - a) (4')
From (5):
T2 = m2 g + m2 a = m2(g + a) (5')
1.3. Solving for the tensions and accelerations
The tangential acceleration "a1" for the mass m1 is
a1 = α r (2)
And
The tangential acceleration "a2" for the mass m2 is
a2 = α r (3)
Therefore
a1 = a2
a1 = a2 = a
Multiplying (4') by r1 and (5') by r2, and
using the formula (1') yields:
r(T1 - T2) = r m1 (g - a) - r m2(g + a)
= I α
Using the relationships (2) and (3), we get:
r(T1 - T2) = r m1 (g - α r) - r m2(g + α r)
= I α
Developing:
r(T1 - T2) = m1 g r - α m1 r2 - m2 g r - α m2 r2
Rearranging to solve for α leads to:
r m1 g - r m2 g - α (m1 + m2) r2 = I α
r m1 g - r m2 g = α ((m1 + m2) r2 + I)
Therefore:
α = r g (m1 - m2)/((m1 + m2) r2 + I)
We have then:
a = α r = g (m1 - m2)/((m1 + m2) + I/r2)
T1 = m1(g - a)
T2 = m2(g + a)
1.4. Particular cases:
1.4.1. At the static equilibrium:
At the static equilibrium (for rotation and translation),
the system is at rest, then its linear and angular
acceleration is zero.
Also, when the system has a constant angular speed, its
linear and angular acceleration is zero: α = dω/dt = 0.
Therefore, the formula (1') becomes:
r(T1 - T2) = I 0 = 0, then
T1 = T2
.
The two torques τ1 = T1 r and τ2 = T2 r are
equal when the system is at rest or at constant speed.
At the static equilibrium:
a = α r = 0
T1 = T2
1.4.2. The pulley is massless:
In the case of the pulley is massless I = 0.
Therefore:
And
T1 = T2 = T, Then:
T = m1(g - a), and
T = m2(g + a)
Hence:
T = m1(g - a) = m1g[1 - (m1 - m2)/(m1 + m2)] =
2m1m2/(m1 + m2)
Massless pulley:
I = 0
a = α r = g (m1 - m2)/(m1 + m2)
T1 = T2 = T = 2m1m2/(m1 + m2)
2. Half Atwood�s machine
It is obtained by eliminating one of the hanging masses and
wrap the free end of the string around the pulley.
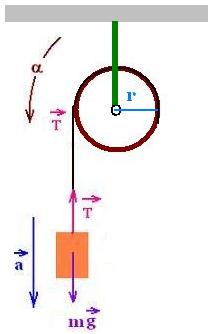
It is particular case of the Atwood's machine described above,
where m2 = 0, T2 = 0, m1 = m and T1 = T.
τ = r T = I α
We have then:
a = α r = r2 g m/(m r2 + I)
T = m(g - a)
a = α r = r2 g m/(m r2 + I) =
g /[1 + (I/m r2)]
T = m(g - a)
3. Falling motion of the pulley
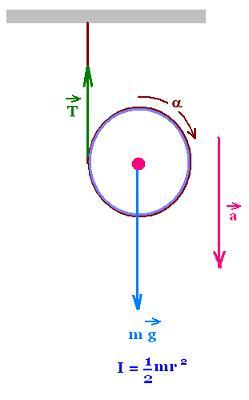
Now, the pulley of mass m is falling while the string
unrolls off a pulley. The results found above still hold:
a = α r = g /[1 + (I/m r2)]
T = m(g - a)
τ = r T = I α
The moment of inertia "I" corresponds to the kind
of a cylinder we use. The maximum moment of inertia
that exists is I = m r2, that corresponds to
a hollow ring; that will reduce a of 50%.
4. Application: A yo-yo
4.1. Dynamics considerations
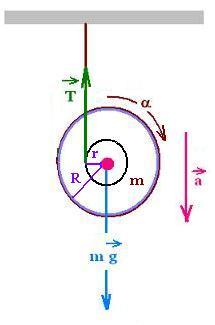
For the acceleration "a", to overcome the limit of 50% of the
acceleration of gravity g, we use a yo-yo with a larger
radius R to increase I with the same mass m. The radius r of the cylinder around which
the string is wrapped is not changed, and therefore the above results
still hold:
a = α r = g /[1 + (I/m r2)]
T = m(g - a)
τ = r T = I α
Let's consider a uniform disk, we have I = (1/2) m R2,
and
write :
β = R/r.
Therefore:
a = α r = g /[1 + (β2/2)]
β = R/r
a = α r = g /[1 + (β2/2)]
In the case of R r, we will have β = 1, and:
a = α r = (2/3) g , and
T = m(g - a) = m (g - 2g/3) = (1/3) mg
4.2. Energy considerations
Using energy considerations, we can find the linear speed
of the center of mass of the yo-yo when it reach a distance
h from an initial position moving downward while the string
unwinds. The moment of inertia of the cylinder of the yo-yo
is I = (1/2) m r2.
At the initial position:
PE = m g h
KE = 0
At the final position:
PE = 0
KE = KE (translation) + KE (rotation) =
(1/2) m vcm2 + (1/2) Icm ω2
As the cylinder of the yo-yo falls without sliding, we have:
vcm = vtangential = ω r
Therefore:
KE = (1/2) m vcm2 + (1/2) ((1/2) m r2) (vcm/r)2
= (1/2) m vcm2 (1 + 1/2) = (3/4) m vcm2
KE = (3/4) m vcm2
Hence
m g h = (3/4) m vcm2 . That is:
vcm = [(4/3) g h]1/2
vcm = [(4/3) g h]1/2
5. Windlass and crate
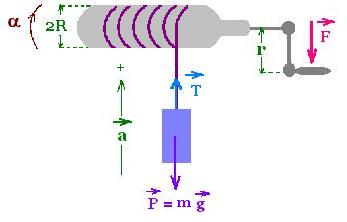
A crate is tied to a rope which is wrapped around a windlass.
The crate has a mass m. The windlass is treated as a cylinder
of radius R ans mass M. We exert a force F on the crank. The whole system
is used to rise the crate as pulling up a bucket of water from a well.
The torque τcrank = F r we exert on the crank is transmitted to
the windlass, where it is exerted a second torque τcrate.
Therefore, Newton's second law for rotation for the windlass is:
Σ τ = τnet = I α =
τcrank - τcrate
I is the moment of inertia of the windlass, and α is its
angular acceleration.
τcrate = T R. Hence:
I α = F r - T R
Newton's second law for the translation for the crate is:
T - mg = m a
Where "a" is the linear acceleration of the crate.
That gives with a = α R :
T = m g + m a = mg + m α R
The above relationship I α = F r - T R becomes:
I α = F r - T R = F r - (m g + m α R ) R =
F r - m g R - α m R2.
Solving for α yields:
α(I + m R2) = F r - m g R . Hence:
α = (F r - m g R)/(I + m R2)
With I = (1/2) M R2, we have:
α = (F r - m g R)/(M/2 + m) R2
α = (F r - m g R)/(I + m R2) =
2(F r - m g R)/(M + 2 m) R2
T = Mg + m a = Mg + m α R
The particular case where there is no force F (no
crank), we have with F = 0:
α = - 2(m g)/(M + 2 m)R (clockwise)
a = α R = + 2(m g)/(M + 2 m) (counterclockwise)
T = I α/ R = I a/R2 = (1/2) M R2 a /R2
= (1/2) M a = (1/2) M 2(m g)/(M + 2 m) =
M m g/(M + 2 m)
Free windlass:
a = α R = + 2 m g/(M + 2 m)
T = M m g/(M + 2 m)
|