Center of mass

1.Definitions

Treating objects as if they were particles is just a good approximation. The term system is used to destribe two or more particles, generally interacting with each other, or an extended object.
To describe the motion of a system of particles or an extended object, we use often a representative point called center of mass. It si defined as:

r_cm = Σ m_ir_i/Σ m_i

m_i and r_i are the mass and the position vector of each point of the object (or each point of the system) respectively. Since Σ m_i = M is the total mass of the system, we can the express the coordinate of the vector position of the center of mass CMby:


r_cm = Σ m_ir_i/M



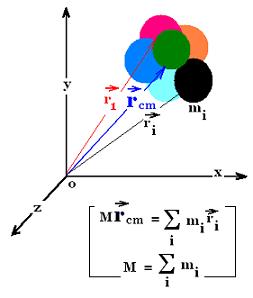
The components of the CM are:
x_cm = Σ m_ix_i/M
y_cm = Σ m_iy_i/M
z_cm = Σ m_iz_i/M

Otfen the system is not a set of distrete particles of mass m_i, but a continuous object. In such case the CM is defined using integral:

r_cm = (1/M)∫rdm

With M = ∫dm, the total mass of the system. Therefore, the components take the forms:
x_cm = (1/M)∫ xdm
y_cm = (1/M)∫ ydm
z_cm = (1/M)∫ zdm

To evaluate these integrals, it is convenient to express the increment of mass dm in terms of the coordinates of the object, often by using the definition of mass density ρ = M/V , V is the volume of the system (or the object).

2. Examples

1. Rod

WE want to find an expression of the CM of a long thin rod with uniform density. For a slice of width of dx, we have a mass of dm = ρ dV = ρ A dx, where A is the lateral area of the rod. Therefore:

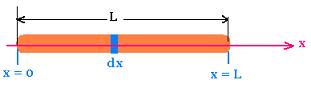
x_cm = (1/M)∫ x dm = (1/M)∫ x ρ A dx = (ρA/M)∫ x dx = (1/2)(ρA/M)[x²] from 0 to L = (1/2)(ρA/M)L² Where L is the length of the rod. Since V = A x L, we have then:

Rod : x_cm = L/2

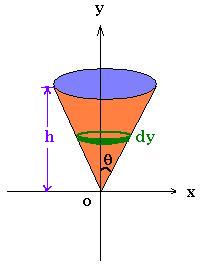
2. Cone

Here the expression of the CM of a cone with fixed angle θ and with uniform density. The CM is located at the y-axis, hence Xcm = 0. For a slice of width of dy, we have a mass of dm = ρ dV = ρ A dy, where A is the area of the disk equal to πx² = (y tg θ)² Therefore:


M = ∫ dm = ∫ ρ dV = ρ tg²θ ∫ y² dy From 0 to h. Then:
M = ∫ dm = ∫ ρ dV = ρ tg²θ ∫ y² dy From 0 to h. Then:
M = (1/3) ρ tg²θ h³
y_cm = (1/M)∫ y dm = (1/M) ∫ ρ tg²θ y³ dy = (1/4)(1/M) ρ tg²θ h⁴
= (1/4) ρ tg²θ h⁴/ (1/3) ρ tg²θ h³ = (3/4) h

Cone : y_cm = 3 h/4

3. Motion of the center of mass

To study a motion of any object or any system of particle, it is complicated to study separately the motion of each part of the object or the system. The simple way is the study of motion of the center of mass. From the definition of the position of the CM, we obtain the expressions of its velocity v_cm and acceleration a _cm by differentiation: v_cm = d(r_cm)/dt = Σ m_idr_i/dt/M = (1/M) Σ m_iv_i Similarly,: a_cm = d(v_cm)/dt = Σ m_idv_i/dt/M = (1/M) Σ m_ia_i

v_cm = (1/M) Σ m_iv_i
a_cm = (1/M) Σ m_ia_i

As for a system with one particle, the only forces that contribute to the motion of the object are the exerted external forces.
If each of all other "j" particles of a system exert a force F_ji on the individual particle "i" of the system, we can write, according to the Newton's second law, for the particle "i":
m_i a_i = Σ F_i = Σ (j) F_ji + ΣF_ext-i Where:
ΣF_i (j) : sum over "i" of all of the interior and exterior forces on the particle "i", and
Σ F_ji (j) is the sum over "j" of all of the j-interior interaction forces on the particle "i", from the j-other particles.
ΣF_ext-i are the sum of all of the exterior forces on the particle "i".

Now, for the whole system of mass M, we write:
M a_cm = Σ (i) m_ia_i = Σ (i) Σ F_i = Σ (i) [Σ (j) F_ji + ΣF_ext-i] = Σ (i)Σ (j) F_ji + Σ (i) ΣF_ext-i]
In the first term: Σ (i)Σ (j) F_ji , according to the Newton's third law, all the forces F_ji and F_ij taken in pairs, cancel out mutally (F_ij = - F_ji), and all the forces F_ii are null. Therefore: Σ (i)Σ (j) F_ji = 0. It remains:
M a_cm = Σ (i) ΣF_ext-i , that is all the esterior forces exerting on the particle "i", and for all the individual particles of the system. We denote this sum of forces by Σ F_ext, and write:
M a_cm = Σ F_ext

M a_cm = Σ F_ext

We recall
internal forces are forces exerted on particles within the system by the other particles within the system, whereas external forces are forces exerted on particles within the system by agents external to the system.

4. Momentum

If we want to know the impact of a moving object of mass m and velocity v, what will be important? mass or velecity? The answer is both of them; and more precisely, their product mv, that is their momentum.

The momentum p of a particle of mass m and velociy v is defined by:

p = m v

v is a vector, and m is a scalr, so P is a vector. The direction of p is the direction of v.
The rate of change in the momentum is:
dp/dt = mdv/dt = ma, that is Σ F_ext, acording to the Newton's second law. The formula dp/dt = Σ F_ext was the original form of the law stated by Newton.
For a system of particles, the momentum is the sum, over all the parts of the system, of individual momenta: p = Σp_i = Σm_i v_i.
Therefore, the rate of change in the momentum is:
dp/dt = Σm_i dv_i/dt = Σm_ia_i = M a_cm, that is equal to ΣF_ext. Hence:
The momentum P of a system affected by external forces only is:

dP/dt = ΣF_ext

5. Conservation of Momentum

If the net force on a particle is zero, then its acceleration is zero according to the Newton's second law, threfore, its velocity is constant. Hence its momentum is constant. In other words, If the net force on a particle is zero, the particle's momentum is conserved.

The moment is a vector, when it is conserved, the moment des not change in time, in direction, and in magnitude.

For a system of particles, if ΣF_ext = 0 then dP/dt = 0, therefore the momenum of the system does not change in time. This is the law of conservation of the momentum.

When the net external force on a system is zero, the total momentum of the system is conserved. If at a certain time the total momentum of a system , that has no external net force, is P_i, and P_f at a later time, we will have P_i = P_f.


Recall
The momentum of an isolated system is conserved

Remark
Even though the total momentum of a system is conserved, the individual momenta of the particles that constitute the whole system may change by internal forces. But the whole system's momentum cannot be changed by internal forces.

6. Impulse

When a ball hits a wall and bounces, its momentum remains constant in magnitude, but changes in direction. The momentum of the wall remains zero because its velocity is null before and after collision. The collision ball-wall lasts a brief time, because of the distorsion of the ball during this collision. The force F_wbthat the wall exerts on the ball is called an impulsive force. The change in direction for the momentum is due to the F_wb. The Newton's second law is written as:
Σ F_ext = F_wb = dP/dt. Integrating gives:
∫ dp = ∫F_wb dt. That is:
Δp = p_f - p_i = ∫F_wb dt form t_i to t_f
The expression ∫F_wb dt form t_i to t_f is called n impulse.