Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Atom in magnetic field
A plane circular current loop of radius r, then
of area πr; carrying an electric
current I, has a magnetic dipole of magnetic moment
vector μ = I A; where A is the vector area normal
to the area A.
Once this magnetic dipole is placed in a magnetic field B,
this field exerts a torque τ = μ x B on the dipole
doing a work on it corresponding to a potential energy
U = - μ . B, in order to align its field to the
magnetic moment.
We want to apply this results to electron in Hydrogen atom,
using the results of the Bohr atom; and therefore show that the
orbital angular momentum L alone of the lectron is not
sufficient to explain anmalous Zeeman effect.
1. Electron orbital angular momentum
1.1. The Bohr magneton
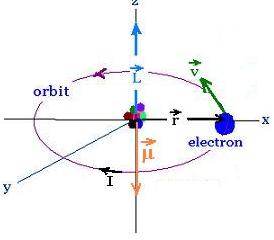
We consider the electron in the Bohr atom
rotating about an axial (z-axis) passing
through the nucleus (proton) as a circular loop
carrying one electron per revolution.
The elecron is of magnitude charge e, mass m, tangential speed v,
orbital angular speed ω angular momentum L, and
orbits with a period T on a circle of radius r
We have:
ω = v/r = 2π/T
I = e/T
A = πr2
Therefore:
μ = I A = (e/T) πr2 =
(e v/2πr) πr2 = e v r/2
Using the definition of the angular momentum L = mvr
yields:
μ = e v r/2 = eL/2m
μ = (e/2m) L
Because the electron charge is negative, the orbital angular
momentum and magnetic moment vectors are opposite
The ratio of the magnitude of μ and L is constant
and equal to μ/L = e/2m. It is called gyromagnetic
ratio.
Using the quantization of the angular momentum : L = mvr = n ħ,
yields:
μ = eL/2m = e n ħ/2m
μ = n (e ħ/2m )
For n = 1, (ground state), the electron orbits on the first layer, hence
the related magnetic moment is called Bohr magneton .
Its magnitude is: μB = e ħ/2m; and its
value is 9.274 x 10- 24 J/T (or A.m2).
Bohr magneton: μB = e ħ/2m
1.2. The correct formula of the magneton
Bohr model gives an expression of the gyromagnetic
ratio μ/ħ = e/2m for the ground state n = 1.
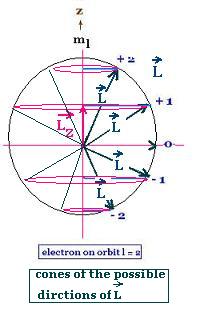
But the Schrodinger results for a hydrogen atom
show that the quantization of the angular momentum
must be written:
L = [l(l + 1)]1/2ħ, and
Lz = mlħ; the projection (component)
of L on the axial z-axis.
where:
l is the orbital quantum number with 0 <= l <= n - 1, and
n is the principal quantum number with n >= 1
ml is the magnetic quantum number with |ml| <= l
The angular momentum L and the magnetic moment μ used by
Bohr must be replaced by their components projection on the axial z-axis.
Also, the quantum number n used by Bohr must be replaced by
ml, so:
Lz = mlħ
μz = ml eħ/2m
Replacing the magnitude charge by its actual charge,
we have: μz = ml eħ/2m
μz = - ml eħ/2m
The Schrodinger formulation predicts for the ground state
with ml = 0 a zero magnetic moment, a value
excluded by the Bohr's model.
Now, if the atom is present in a magnetic field B directed
along the z-axis, the interaction of this field with the magnetic
moment μ gives rise to the torque *tau; that corresponds to a
potential energy for the field U = μ · B = - μz B
= ml eħB/2m . That is the orbital magnetic interaction
energy:
U = ml (eħ/2m) B = ml μB B
2. The effect of the magnetic field on the orbital state of the electrom
The electron rotating on an orbit about z-axis
crossing the nucleus has a (quantum) mechanic angular momentum L and,
because it is charged, a corresponding orbital magnetic moment μ. L and μ are
always antiparallel. The quantization of L leads to set that
its z-component Lz = mlħ. For a principal
quantum number n, we have (n - 1)n/2 values of l; and for
each l, we have (2l + 1) values of ml. The energy
of the electron depends on its principal quantum number
only, that is En = - 13.6 eV/n2. Therefore, without
a magnetic field, all the (n-1)n/2 x (2l+1) states would have the same energy
En, that is all these states would be degenerate.
For an orbital state l, we have (2l + 1) values of ml, then
(2l + 1) values of μz, and (2l + 1) values of Lz.
All these (2l + 1) states are shown and split from each other
by a magnetic field. The effect of the magnetic field is to remove this
degeneracy, that is to split the energy of each orbital state by an amount
of U =ml μBB.
In the presence of a magnetic field, the energy of an electron
in the state l, will be split into (2l + 1) distinct energy levels.
Two adjacent levels are separated by the energy μB B.
Example:
For a hydrogen atom at the state n = 2, the electron is
either in the orbital state "s" (l=0) or the orbital state "p" (l=1).
we have l = 0 and l = 1.
No magnetif field:
E2 = -13.6/4 = - 3.4 eV
With magnetic field:
If the electron orbits in the state "s", then:
l = 0 : ml = 0
E = - 3.4 eV + 0
If the electron orbits in the state "p", then:
l = 1 : ml = -1, 0, +1
E = - 3.4 eV - μB B
E = - 3.4 eV + 0
E = - 3.4 eV + μB B
3. Larmor precession
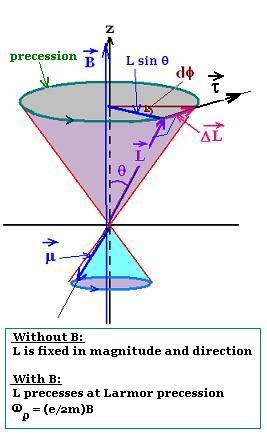
The atom is placed in an external magnetic field B directed along
the axial z-axis. The magnetic moment μ (proportional
to the orbital angular momentum L: μz = - (e/2m)L)
undergoes a torque parallel to ΔL = μ x B. This torque,
perpendicular to the orbital angular mmentum L, tends to line up
the magnetic moment with the magnetic field B along the z-axis.
Therefore, the torque exerted produces a change
in orbital angular momentum dL which is perpendicular to that angular
momentum L, according to the law: τ = dL/dt. This change in orbital angular momentum
causes the magnetic moment to precess around the direction of
the magnetic field. This is called Larmor precession.
If θ is the angle where L is fixed, and φ
the precession angle, we have:
τ = ΔL/Δt = dL/dt = (L sinθ) dφ/dt
Since τ μ x B = μ B sin θ, and μ = (e/2m) L
Therefore:
μ B sin θ = (L sinθ) dφ/dt, then:
μ B = L dφ/dt, or dφ/dt = (B/L)μ = (e/2m) B
Setting ωp = dφ/dt,
the expression of the Larmor precession is:
ωp = (e/2m)B
|
|