
1. Definitions
The original statement of the Newton's third law is:
Law III. To every action there is always opposed an
equal reaction.
That is: whenever two bodies interact, the two forces that they
exert on each other are always equal in magnitude and opposite
in direction.
Newton's third law applies to an interaction between
two objects, whereas the first and second Newton's laws apply
to a single object.
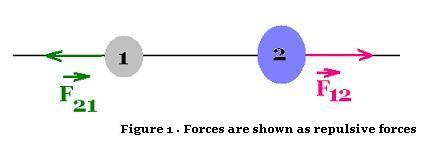
If object 1 exerts a force F12 on object 2, then ,
necessarily, object 2 exerts a force F21 on object 1.
Newton's third law states that these two forces are equal and
opposite, or
These two forces are equal in magnitude and opposite in direction. One
is called action force, the other is called reaction force.
The two forces Fab and Fba form an action-reaction pair.
2. Force symbol Fab
Note that forces occur in pairs. A single force cannot exist.
Two subscripts a and b are required on the force symbol Fab. The first
subscript a denotes the object that exerts the force, and the second subscript
b denotes the object on which the force acts.
The action-reaction pair is indicated by the reversal of the subscripts
on the forces symbols.
3. Examples
3.1. Normal force
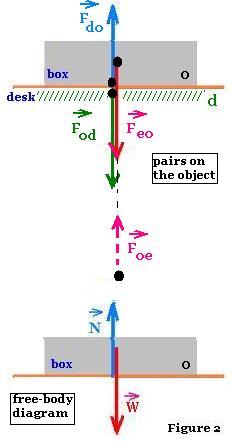
The force N is called the normal force and the force W is called
the weight of the object o.
Is the couple (N,W) an action-reaction pair?
N is the force exerted by the desk d on the object o: Fdo, wheras
W is the force exerted by the earth on the object o: Feo.
We dont have a reversal of subscripts, therefore the two forces N and W do not
constitute an action-reaction pair.
These two forces are equal and opposite, without forming
an action-reaction pair.
The two forces in the Newton's third law never occur in the same
free-body diagram. This is because a free-body diagram shows
forces acting on a single object.
3.2. Solved example: Many objects
Suppose that two objects are placed on a floor, with the
object 2 on top of the object 1 (figure 3). We want to
determine the reaction of the floor on the object 1.
3.2.1. Forces acting on the two objects
All the five forces are represented for the two objects.
Three for the object 1:
- Fe1: The weight of the object 1, that is the force exerted
by the earth on the object1.
- Ff1: The force exerted by the floor on the object1.
- F21: The force exerted by the object 2 on the object 1,
because there is an interaction between them,
and two forces for the object 2:
- Fe2: the weight of the object 2, that is the force exerted
by the earth on the object2.
- F12: The force exerted by the object 1 on the object 2,
that is the reaction for the action F21 (or the action
of the reaction F21).
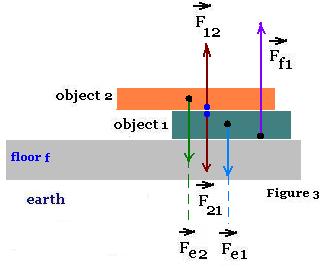
All the forces acting on the objects 1 and 2 are drawn. Among these forces,
we have one action-reaction pair: (F21, F21).
Note that Newton's third law applies to an interaction between two objects.
3.2.2.Related free-body diagrams
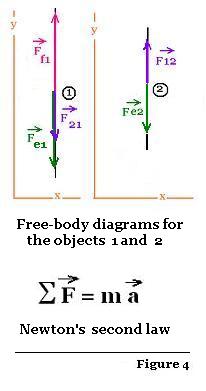
Now, to apply Newton's second law, we need to separate
the objects, and draw a free-body diagram for each object alone .
A free-body diagram shows forces acting on a single object.
object1:
The vector sum of the three forces is:
Fe1 + Ff1 + F21 = m1 a1
Where m1 and a1 are the mass and the
acceleration of the object 1 respectively.
Since the object 1 is at rest, we have a1 = o; therefore
Fe1 + Ff1 + F21 = 0. Thus:
Ff1 = - Fe1 - F21
object2:
The vector sum of the two forces is:
Fe2 + F12 = m2 a2 = 0,
because a2 = 0. Thus:
F12 = - Fe2
If the object1 weighs 8.00 Newtons and the object 2
weighs 10.0 Newtons, what is the magnitude of the
reaction of the floor on the object 1?
Ff1 = 18.00 Newtons.
|