α-decay and dose absorbed

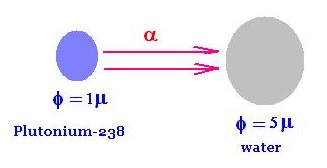
We are interested in evaluating the absorbed dose 
of the α-decays projectile particles emitted from 
a Plutonium-238, by a sample of water.

1. Plutonium element

Let's consider the Plutonium element:
Symbol: Pu
Atomic Number: 94
Number of Protons/Electrons: 94
Number of Neutrons: 150
Atomic Mass: (244.0) amu 
Classification: Rare Earth (actinide series: synthetic or man-made).
Density at 293 K (200): 19.84 g/cm3 = 
19.84 x 10-3 kg/10-6 m3 = 
19.84 x 103 kg/m3 

Isoptopes:

-- Plutonium-244, the most stable, of half-life 
of about 80 million years. 
-- Plutonium-240, with a high rate of spontaneous fission.
-- Plutonium-239, the most useful for nuclear weapons, 
fissile as Plutonium-241 .
-- Plutonium-238 has a half-life of 88 years and emits 
alpha particles. It is e heat source in thermoelectric generators.

We will focus on the istope 238.

2. Moles and Avogadro number

Avogadro number = 6.023 x 1023
1 uma = 12 x 10- 3 /12 Nav = 
1.66054 x10-27 kg.

We neglect the mass of the electrons, thus  
the mass considered is the mass of the 
nucleus.

1 mol of Pu weights 244.0 grams. That is, 1 gram of Pu 
contains 1 mol/238.0 nucleus = Nav/238.0  nucleus. 

If we consider a mass m (grams) of Pu, then, this mass 
corresponds to: 
m x Nav/238.0  nucleus.

generally,

The number of nuleus N in a mass of m (grams) 
of an element of atomic mass "A"(grams) is:

N = m x Nav/A  nucleus
m and A in grams. 

3. Density

The density d is equal to m/V.
For a sphere of diameter D, V = (4/3)*π(D/2)3, we
have:
m = d V = d (4/3)*π(D/2)3
And:

N = d (4/3)*π(D/2)3 x Nav/A 


A 1 µm diameter sphere of Pu contains:

N = d (4/3)*π(D/2)3 x Nav/A = 
19.84 x 103 kg/m3 (4/3)*π(1 x 10-6/2)3 m3
x 6.023 x 1023/238.0 x - 3 kg 
= 2.6 x 1010 nucleus.


This ball of Pu is going to decay. 

4. α-decays from a Plutonium-238

At time t0 = 0, the number of nucleus that is available is 
N0 = 2.6 x 1010 nucleus.

By decaying, the remaining number of nucleus at the 
time t is N(t) = N0 exp {- λt}

The half of remaining number of nucleus N0 /2 
corresponds to the half-life th:

N0/2 = N0 exp {- λth}
Then: 1/2 = exp {- λth} , hence:
- log 2 = - λ th, thus:
th = log 2 /λ

For the Plutonium-238, we have the half-life th = 88 years 
= 88 x 365 x 24 x 60 x 60 seconds = 2.8 x 109 s
Therefore 
λ = log 2/ th = 2.50 x 10- 10 s-1 

5. Activity of the α-decays from a Plutonium-238

The activity is:

A(t) = - dN(t)/dt = λ N0 exp {- λt} =  λ N(t)

The initial activity is A(0) =  λ N(0) = λ N0
For the Plutonium-238, A(0) = 2.50 x 10- 10 x 2.6 x 1010 = 
6.5 nucleus/s = 6.5 decays/sec = 6.5 Bq 

Since:
1 Ci = 3.70 x 1010 Bq = 
3.70 x 1010 decays/s, 
then:
A(0) = 6.5 Bq = 6.5 Ci /3.70 x 1010 = 
1.76 x 10- 10 Ci

If each α emitted has an energy of 5 MeV = 
5 x 106 x 1.6 x 10-19 joules = 

The  activity at t = 1 µs  is A(1 µs) =  
λ N0 exp {- λ1 µs}
For the Plutonium-238, A(1 µs) = 
2.50 x 10- 10 x 2.6 x 1010 exp {- 2.50 x 10- 101 x 10- 6} = 
6.5 exp {- 2.50 x 10- 16} = 6.5 x 1 =  6.5 decays/sec = 6.5 Bq 
 = 6.5 Bq = 1.76 x 10- 10 Ci

 

6. Dose absorbed and RBE

If each α emitted has an energy of E = 5 MeV = 
5 x 106 x 1.6 x 10-19 joules = 
8 x 10-13 joules, the dose deposited in a 
sphere of 5 µm of diameter in water is:
D = E/V

V = (4/3)π (D/2)3 = (4/3)π (5 x 10-6/2)3 
= 6.55 x 10-17 m3

The density of water is equal to 1 kg/dm3 = 
1 kg/ -3m3 = 
1000 kg/ m3 , d = m/V = 1000 kg/ m3
Therefore:

V (in m3) corresponds to a mass of M = 1000 x V Kilograms = 
1000 x 6.55 x 10-17 = 6.55 x 10-14 Kilograms

Therefore:
D = E/M = 8 x 10-13 / 6.55 x 10-14 Joules/Kilograms 
= 12.20 Joules/Kilograms

Since:
1 Joule/Kg = 1 Gy

The dose deposited by one α particle of 
5 MeV energy due to the decay of a nucleus of Plutonium-238,  
in a sphere target of water of 5 µm of diameter is 12.20 Gy.

For this nucleus, we have an activity of A(0) =  6.5 α-decays/second

Then: 6.5 α deposit 6.5 x 12.20 Gy = 79.3 Gy/second

1 year = 365 x 24 x 60 x 60 seconds = 3.15 x 107 s, so:
 6.5 α deposit 79.3 Gy/second = 3.15 x 107 x 79.3 Gy/year = 
 2.50 x 109 Gy/year
 
 Since 1 rad = 0.01 J/kg = 0.01 Gy, we have:
 D = 12.20 Joules/Kilograms = 12.20 Gy = 12.20 x 100 rad = 1220.0 rad 
 All the dose deposited is absorbed., therefore, 
 the Equivalent dose (rem) = RBE x absorbed dose(rad)
 
 The RBE of α particle = 20 rem/rad
 Therefore,
 The Equivalent dose (rem) of the one α particle emitted 
 and absorbed by the sample of water is:
 20 x 1220.0 rem = 24400 rem
 
 During a year from the Plutonium sphere, we have 
 2.50 x 109 Gy/year, that corresponds 
 to the dose:
 Dose = 2.50 x 109 Gy/year = 2.50 x 1011 rad /year = 
 2.50 x 1011 x 20 rem/year = 5.0 x 1012 rem/year
 
 

Terminology:
 
 RBE: Relative Biological Effectiveness
 in Sv/Gy = rem/rad
 Sv = Sievert
 rem = Röntgen equivalent for man
 
 1 Gy (gray) = 1 J/Kg
 1 rad = 0.01 Gy