Measurements in Physics
1. Some definitions
Physics involves logical reasoning. In Physics, we use
numbers to have an idea about quantities.
A book weights 1.20 kilograms and has 20.35 centimeters length and 23.0
centimeters width.
The related digits 1.20, 20.35, and 32.0 are numbers.
kilograms and centimeters are called dimensions.
Each dimension has a unit. We can use meters,
centimeters or kilometers to mesure a length. In science, we use meter (m)
for length, kilogram (kg) for mass and second (s) for time; these units
come from The International System (SI) standards;
wich contains seven base units.
Derived units like velocity are the combination
of two or more units from the base units of the SI.
It happens that others quantities are expressed in others units, but these
others units have their equivalent in the base units of the SI standard.
A velocity is expressed in meter per second (m/s).
A force is expressed in Newtton (N). But the Newton stands for One kilogram
multiplyed by One meter divided by One second (1 kg . 1 m / 1s)
2. Measurements
|
Prefixes in metric units
The average distance between an electron and the
nucleus in an atom is 0.000 000 000 05 m
This number is very small! we write it as: 0.5 x 10- 10 m
When we say that the atomic number of the hydrogen is 1; that means the
weight of 602 300 000 000 000 000 000 000 = atoms in 1 gram.
This number is very large!. We wrte is as 6.023 x 10+23.
We express then the large and the small numbers, difficult to read and
to write in powers of ten. We use some prfixes to symbolise some powers of
ten as shoown at right:
|
| Power | Prefix
| Abbrviation |
| 10- 18 | atto | a |
| 10- 15 | femto | f |
| 10- 12 | pico | p |
| 10- 9 | nano | n |
| 10- 6 | micro | μ |
| 10- 3 | milli | m |
| 10- 2 | centi | c |
| 10- 1 | deci | d |
| 10 1 | deca | da |
| 10 3 | kilo | k |
| 10 6 | mega | M |
| 10 9 | giga | G |
| 10 12 | tera | T |
| 10 15 | peta | P |
| 10 18 | exa | E |
|
Conversions
0.5 x 10- 10 m = 0.05 x 10- 9 m = 0.05 nono-meter.
6.023 x 10+23 = 602,300 x 10+18 = 602,300 exa-meters.
3. How to convert?
Rule:
If We have a unit X and we want to convert it in the unit Y, just multiply
X by Y, build the conversion factor by deviding the result by Y expressed
in X and simplify by X. Here are some examples:
Example 1:
cm = ? m
cm is provided. m is needed. The steps are:
Multiply cm by m → cm x m
Build the conversion factor : devide the result by m
expressed in cm ( that is 100 cm) → cm x m /100 cm
Simplify by cm (the two cm in the numerator and the deminator
cancel)→ m /100 = 1 x 10 -2 m
Example 2 :
4.5 kg = ? gram
4.5 kg = (4.5 kg x gram)/ gram = (4.5 kg x gram)/ 10 -2 kg = 4.5 kg x 10 +2 grams.
3. Accuracy and precision
As a human being, measuring a dimension is not free of
error. But it's important to minimize errors to reach an accurate
result. When we measure, we deal with thrre kind of errors:
- Human errors
- Method (or computational or technique) errors
- Instrumental error
Human errors come from personal bias or carelessness in reading
instrument, or recording observations, or mathematical calculations.
The solution for this problem is to repeat the measurements in order to
be certain that they are close to the true value.
The second source of error is due to a method (technique) we utilize
to set a result.
The cause of the instrument error is the instrument itself.
All those three experimental sorts of errors are
systematic. An error is random when
it is beyond our decisions, that is unknown and unpredictable
varaiations or changes in experimental situations such as
a temperature fluctuation of the environement.
Example:
 Human errors:
To read 20 cm while measuring the width of a book we make
a mistake and consider 8 (inches!).
Human errors:
To read 20 cm while measuring the width of a book we make
a mistake and consider 8 (inches!).
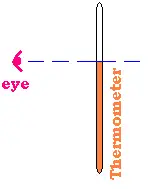
Method errors: The well known is the parallax;
that is the error related to the position of the experimenter regarding the
dimention to measure. To give a good value of the temperature, the best position is that the thermometer
is parallel to the face of the observer and the level of the mercury perpendicular to the eye.
Instrument error: We cannot have a good measured
value from a damaged equipments and devices.
3.1. Acuuracy
The measured dimension is never perfect. But when those three kind of arrors are
minimized, we say that we have a good accuracy.
The accuracy is related to "how close we are to the true or ideal or
accepted value". We can have a high accuracy without be precise.
The precision is another factor. It refers to the degree
of exactness when we make a measurement.
The accuracy of a measurement is expressed by the percentage error:
Accuracy = percentage error =
100 x |AcceptedValue - MeasuredValue|/AcceptedValue (%)
3.2. Precision
The precision is related to the measuring instruments. The more
an instrument contains divisions, the more the value becomes precise.
We get a precise result among repeated measurements.
Example:
If we measure the length of a book with a meterstick divided into millimeters
we get a precise value than if it was marked in centimeters.
The precision of a measurement is given by the expression of the
Average deviation or the Standard deviation of the obtained
results:
Average deviation = Σ|AbsoluteDeviation|i/n [from i=1 to i=n]
= Σ|x - xi|/n [from i=1 to i=n]
Where:
n is the number of the repeated measurements
x is the avarage value of the measurements
x - xi is the absolue deviation of the individual result.
A good estimation depends then on the digit we consider
for the measurement.
|