Contents
© The scientific sentence. 2010
|
Electrical Bridges
1. Galvanometer:
We use a galvanometer as both a voltmeter and an ammeter. As a voltmeter, a resistor with high resistance is
placed in series with the galvanometer to have a voltmeter. The electric current passing through the
circuit is then very small. As an ammeter, a resistor with a small resistance is placed in parallel with the
galvanometer.
2. Kirchhoff's laws
Kirchhoff's Voltage Law (or Kirchhoff's Loop Rule) results from the conservation of energy
in a circuit. It states that the total voltage around a closed loop must be zero; ΣUi = 0.
Kirchhoff's Current Law results from the conservation of charge. It is applied for nodes
in a circuit where the sum of all the currents is zero: ΣIi = 0.
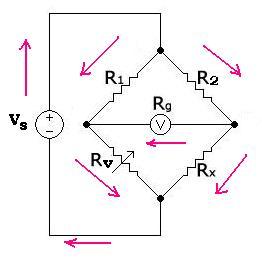
3. Weatstone bridge:
The Wheatstone bridge is used to measure an unknown resistance.
In this figure, Rx is the unknown value of a resistance to be measured,
and Rv is a variable resistor. The idea is to vary the resistance Rv until
the galvanom�tre (resistance Rg and voltage Vg) indicates zero.
Once this condition is achieved, we can find the value of Rx. Indeed:
We have:
Ig + I1 = Iv
Ig + Ix = I2
R2 I2 + Rg Ig - R1 I1 = 0
Rv Iv - Rx Ix + Rg Ig = 0
Ig = 0 implies:
I1 = Iv
Ix = I2
R2 I2 = R1 I1
RvIv = Rx Ix
Then:
Rx = Rv Iv / Ix = Rv I1/I2 = Rv R2/R1
Rx/Rv = R2/R1 (1)
We can also express the value of the voltage Vg depending
on the value of the voltage source Vs:
Vs = R1I1 + Rv (I1 + Ig) → I1 = (Vs - RvIg)/(R1 + Rv) (a)
Vs = R2I2 + Rx (I2 - Ig) → I2 = (Vs + RxIg)/(R2 + Rx) (b)
We have:
Vg = R1I1 - R2I2
With the equations (a) and (b), we obtain:
Vg = Vs(R1/(R1 + Rv)) - Vs(R2/(R2 + Rx)) - Ig[R1Rv/(R1 + Rv) + R2Rx/(R2 + Rx)]
As Ig is very small, then the term if Ig is negligible, we have finally:
Vg = [R1 / (R1 + Rv) - R2 / (R2 + Rx)] Vs
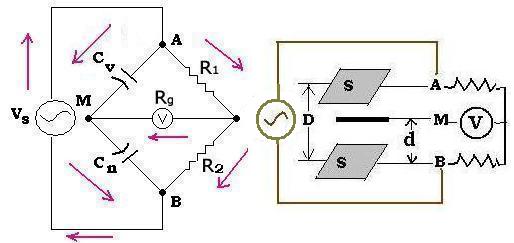
4. Modified Weatstone bridge: Sauty Bridge:
It is used to measure a level or pressure of a liquid in a container. It
contains two capacitors and two resistors.
We have the same reasoning as for the Wheatstone bridge. Since the current is alternatif, the
expresions of the currents and voltages are effective quantities. The impedance of a capacitor is
Z = 1/Cω (ω is the frequency of the altenatif current), as in the relationship (1), we have:
R2 / Cω = R1/Cn or
Cn / Cv = R1/R2 (2)
The expressions of the two capacitors are:
Cn = ε0 εr S / d
Cv = ε0 εr S / (D - d)
Then:
Cv/Cn = d/(D - d) = (d - 1) /D
The distance "d" is fixed and known, so is the value of Cn. If the distances "D" changes;
then the distance "D - d" between A and M changes; that gives a new value of Cv; according
to the value of Cn.
The expression, as for the Weatstone bridge, of the voltage V takes the expression:
V = [Cn / (Cv + Cn) - R1 / (R1 + R2)] Vs
We can write:
V = [1 / (Cv / Cn + 1) - R1 / (R1 + R2)] Vs = [(D - d) / D - R1 / (R1 + R2)] Vs
V = [(1 - d/D) - R1 / (R1 + R2)] Vs
For each displacement "D - d" or "D", we have directly a value measured in the galvanometer V.
This is the principle of a flow transmitter of a fluid.
3. Example:
D = 10 cm , d = 4 cm, R1 = R2 = R3 = 5 kΩ, Vs = 110 Volts
V/Vs = (10 - 4)/10 - 5/(5 + 5) = 0.6 -0.5
V = Vs/10 = 110/10 = 11 Volts
For a distance of 6 cm, we get 11 Volts in the galvanometer.
|
|