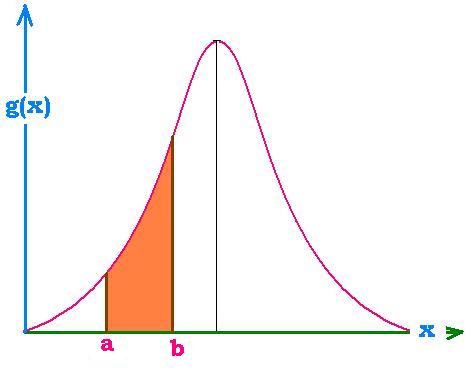In this example, we want to find the value of the integral between the two values a and b. We will use the Monte Carlo method MC and the Rectangle method, called Riemann sum. The related colored part represents the probability that an event would occur between the two values a and b. The first technique uses random numbers and the second method uses Rectangles. For the second method, we sum the values of successive and discrete numbers Σexp(x_i)²; whereas the Monte Carlo technique uses the sum of random numbers Σ exp(x_r)² generated by chance. The number of iterations for MC method is the number of the steps for the Rectangle method. The Gaussian (Normal distribution) exp(-x²) must be normalized to 1 in order to represent the probability density; that is ∫ C dx exp(- x²) = 1. This leads to C = 1/2 sqrt(π).
Source code