RAMAN effect
1. The electric dipole moment
The term polarization is directly related to
the electric field in place.
Let's talk first about the polarization.
Consider two charges -q and +q, separated
with a distance d. The electric dipole moment
P is defined as the product of q and the vector d.
The direction points from (-) to (+).
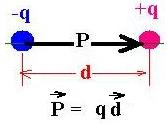
Remark that the net charge qnet = 0.
The polarization vector of a matter is the sum of the related
dipole moments per unit volume.
If a set of molecules is free, these molecules are
oriented whatever in space, that is the vector p takes
a randum direction. However, if an elecric field is
applied in the medium of these molecules, each dipole p
of a molecule tends to orientate itself in order to get
aligned according to the direction of the applied electric
field experienced by this molecule.
2. The related polarizability
Not that even in the absence of an electric field,
a molecule has its own permenent dipole moment induced by the local
electric field due to the electronic cloud.
Some of the molecules are polar, others are nopolar.
These two terms are related to the net dipole moment.
Examples:
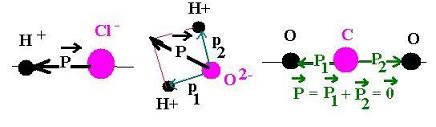
- For water, the dipole moment is present; this molecule is polar.
(the net dipole is not null)
- For carbon dioxide, the dipole is hidden; this molecule is nonpolar.
(the net dipole is null)
The polarizability defines the possibility or the ability of
a molecule to get its electronic cloud distorted; then give
rise to a diplole moment.
For the first approximation, we assume that the
field E is proportional to the dipole moment. We can
write
P0 = α0.Elocal
Where:
P0 is the permenent dipole moment, and
α0 the associated polarizability.
3. Example: the carbon dioxide molecule CO2
Let's consider the example of the carbon dioxide CO2.
Its molecular geometry is linear and triatomic. Each of the
carbon-oxygen double bonds is polarized toward the more
electronegative oxygen.The related dipole moments are of the
same magnitude and aligned tail-to-tail. They exactly balance
each other and their sum is zero.The carbon dioxide is a
nonpolar molecule.Hence, P0 = 0.
Here are the three (or four) vibrational modes for
the carbon dioxide molecule:
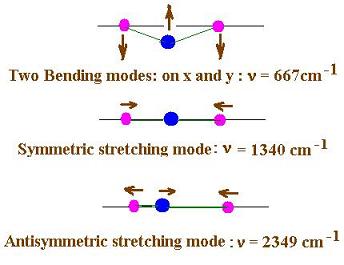
4. The Raman scattering
Even if the molecule has a null polarization (no
permanent dipole moment), it has a polarizability.
A dipole moment in this molecule can be induced by
an external electric field.
The polarizability α vibrates the same way the molecule does.
Let's write :
α = α0 + αvibcos (ωvibt) = αvibcos (ωvibt)
That is the polarizability is a time-varying on the vibrational
frequency of the molecule: ω.
And the external applied ( appl) field has this form:
E = E0 cos(ωapplt)
Then, the dipole moment experienced by the CO2 molecule is:
p = αE
= αvibcos (ωvibt) . E0 cos(ωapplt)
= αvib. E0 . cos (ωvibt) . cos(ωapplt)
From the relation:
cos(a+b) + cos(a-b) = 2. cos a . cos b ,
we get:
p =(1/2) αvib E0 [cos(ωappl + ωvib)t + cos(ωappl - ωvib)t]
The dipole moment oscillates with frequency components:
cos(ωappl + ωvib) and cos(ωappl - ωvib)
If a stream of photons ( then electric field E) collides with a
molecule, three process may occur:
- If the collision is perfectly elastic, that is the incident frequency
is equal to a transition molecular energy level; photons will be deflected
without change in frequency, then with ωvib, in this case,
energy is exchanged between photon and molecule. The process is called
Rayleigh scattering. ( Most of the scattered light)
- If the collision is inelastic, the molecule will change energy (discrete
of course) with the incident photon, that is the frequency is changed.
The molecule gains energy by the term :
ωappl + ωvib : Antistokes
and loose energy by the term:
ωappl - ωvib : Stokes
Hence the molecule will scatter the two related photons:
-- Stokes scattering with decreased frequency.
-- Anti-Stokes scattering with increased frequency.
That is the Raman scattering.
(In small fraction of the scattering: about 1 in 107,
of the incident photons)
Raman scattering is discovered by the physicist Chandrasekhara Venkata
Raman in 1928.
|

