Electric dipole: Selection rules

1. Potential energy stored in a dipole

A electric dipole is a distribution of two charges 
of equal magnitude and oposite sign + q and - q. The 
electric dipole moment P is by definition a vector 
equal to:

P = q d

d is the distance between the two charges. The direction of 
P is the ne of d, that is fron -q toward +q.



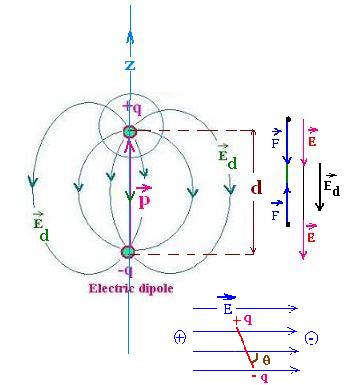Two Coulomb forces attracting each other F+q and F-q 
that give a net zero force take place at each point charge. According the 
F = q E law, these forces correspond to the electric fields E+q 
and F-q that give a net electric field Fd directed 
from -q toward +q.

An exterior electric field E on the dipole produces a torque 
on the dipole p, that is equal to the cross product of p and E: 
τ =  p x E = pE sin θ 
and tends to align it on the same directionas the electric field. 
this rotating work given to the dipole is equal to the potential energy 
stored in the dipole:
p and E: U = ∫ τ d&theta'; from 0 to θ = - pE cos θ = - p . E 
wich is equal to the scalar product of p and E.

The potential energy stored in the dipole is:

U =   - p . E 

Let's write U = V(d). For an electron in the atom q = e:
V(r,t)  = - e r.E 
or: 

V(r,t) = - e E r.ê 
ê is the unit polarization vector of E.

2. The Electric Dipole Approximation

The Electric field that is considered here correspond to the one 
of an electromagnetic radiation regarding transitions between 
different atomic energy levels. The related wavelength much larger 
than the typical size of an atom.

The expression of the oscillating electric field that perturbs 
the dipole field can be written as:
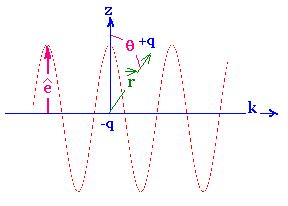
E = Eoo cos{i(k R - ωt)}, or 
E (R,t) = Eo exp{i(k R - ωt)} + exp{- i(k R - ωt)}
R is the vector position where we locate the wavefunftion 
that brings this electric field (as an electromagneic wave 
where we take into account just the the electric field: E>>B)

Now consider the sizes involved: 
The perturbing wave function E(R,t) corresponding to an optical
transition 
has dimensions (λ = 2π/k)  on 100 nm; that is 1000 
times shorter that the dimensions involved in an atomic wavefunction 
wich has dimensions on the order of the angstrom. Therefore 
the term k.R = 2πR/λ is very small and it can be
geglected. Hence, we use the appriximation that E is 
constant in space (but not in time).This is known as the 
Electric Dipole Approximation. In other words, we 
use just the first term, that is "1" in the following development:

exp{ikR} = 1 + ikr + ...

Therefore, the expression of the oscillating electric field is:
E (R,t) = E(t) = Eo [exp{iωt} + exp{-i ωt}]
and the expression of the potential energy of the dipole is:
V(t) = - e Eo r.ê  [exp{iωt} + exp{-i ωt}]


V(t) = - e Eo r.ê  [exp{iωt} + exp{-i ωt}]

3. Dipole matrix elements

We have seen the Fermi's Golden rule gives the 
following transition probability:

Pi → f = (2 π/ℏ) |<f|V|i>|2 δ(Ef - Ei + ℏω) +  
(2 π/ℏ) |<f|V+|i>|2 δ(Ef - Ei - ℏω)

For a perturbation V(t) with:
V(t) = 0 if t<= 0
V(t) = V exp{iωt} + V+exp{-iωt} if t> 0

Here: V = V+ = - e Eo r.ê

Therefore, <f|V|i> corresponds to the following dipole 
matrix elements: - e Eo <f|r.ê|i>

Now, we are going to calculate <f|r.ê|i>.
Recal: r is the vector of the dipole )  = q r = - e r), and
ê is the unit polarization vector of E.

We have three cases:

3.1.Linear polarized light

The wave vector k is perpendicular to the z-axis, and 
r is parallel to the z-axis, therefore:
r.ê = z = r cos θ = (4π/3)1/2 r Y10(θ,φ)



 <f|r.ê|i> = (4π/3)1/2 <f|r Y10(θ,φ)|i>
 

3.2.Right and left circular polarized

 The left or right hand circular polarized are 
 expressed as:
 Left: 
 r.ê = - (2)- 1/2(x + iy) = - r(sin θcost φ + sinθ sin φ) = 
 - r sin θ exp{+i&thi;} = - (4π/3)1/2  r Y1+1(θ,&phi:)
 
 Right:
 r.ê = +(2)- 1/2(x + iy) = + r(sin θcost φ - sinθ sin φ) = 
 + r sin θ exp{- i&thi;} = + (4π/3)1/2  r Y1-1(θ,&phi:)

4. Selection rules

An eigenstate i> is written as the product of a radial part 
and angular part:
i> = Rnl(r) Yml (θ,φ) 
The angular part is written as the product of the polar part and 
the azimuthal part:
Yml (θ,φ)  = [(2l+1)(l-m)!/ 4π(l+m)!]1/2 Pml(cos θ) exp{imφ}

Therefore:

<f|r.ê|i> = (4π/3)1/2 <f|r Y1q(θ,φ)|i> = 
= 
(4π/3)1/2 
∫∫∫ r r2 dr sinθ dθ dφ R*n'l'(r) Y*m'l' (θ,φ) Y1q(θ,φ) 
Rnl(r) Yml (θ,φ) 

=  (4π/3)1/2 ∫ r3 dr Rn'l'(r) Rnl(r) ∫ ∫sinθ dθ dφ 
Y*m'l' (θ,φ)  Y1q(θ,φ) Yml (θ,φ) 


According to:
Ym*l (θ,φ) = (-1)mY-ml (θ,φ), we have:

<f|r.ê|i> = (4π/3)1/2  ∫ r3 dr Rn'l'(r) Rnl(r) ∫ ∫sinθ dθ dφ (-1)m 
Y- m'l' (θ,φ) Y1q(θ,φ) Yml (θ,φ) 

= (-1)m (4π/3)1/2 [(2l+1)(l-m)!/ 4π(l+m)!]1/2 
[(2x1 + 1)(1 - q)!/ 4π(1 + q)!]1/2 [(2l'+1)(l'- m')!/ 4π(l'+ m')!]1/2
∫ r3 dr Rn'l'(r) Rnl(r) ∫sinθ dθ P- m' l' (cosθ) P1 q(cos θ)Pm l (cos θ) 
∫ exp{- im'φ} exp{i qφ} dφexp{imφ}

The azimuthal part gives:
∫ exp{- im'φ} exp{i qφ} dφexp{imφ} = 
∫ dφexp{i(m + q - m')φ} 
from 0 to 2π

This integral is null, unless m + q - m' = 0, therefore:
∫ exp{- im'φ} exp{i qφ} dφexp{imφ} = 
∫ dφexp{i(m + q - m')φ} = δ(m + q, m')
from 0 to 2π 

For this polarization, we have q = 0,
Thus:Δm = 0

The polar part gives:
∫sinθ dθ P- m' l' (cosθ) P1 q(cos θ) Pm l (cos θ) 
= 2 [l'0,l0,l0]2
Where [l'0,l0,l0] is the coefficient related to the Wigner 
3j symbol. 

This coefficient is nonzero only when:
l' + 1 + l is an even integer, l and l' are >= 0 , and |l' -1 | <= l <= l' + 1

That is: 
l' - l = + 1 or -1 only
or Δl = +1, -1
Δl = +1, -1


Similarly, for the circular left and right polarization we 
have with q = -1 or +1:

∫ exp{- im'φ} exp{i qφ} dφexp{imφ} = δ(m + q, m')
from 0 to 2π 
That gives:
Δ m = + 1 or - 1.
Δ m = + 1 or - 1.

And the two clebsh Gordan coefficients:
[l'0,l-1,l0] and [l'0,l+1,l0]
That lead to 
Δl = +1, -1
Δl = +1, -1

Therefore, the selection rules for un electric dipole are 
the following:
Δ m = 0, + 1 or - 1
Δl = +1, -1

Electric dipole:
selection rules:
Δ m = 0, + 1 or - 1
Δl = +1, -1