Quantum Mechanics
Schrodinger equation
Quantum Mechanics
Propagators : Pg
Quantum Simple Harmonic
Oscillator QSHO
Quantum Mechanics
Simulation With GNU Octave
© The scientific sentence. 2010
|
|
Rotation in Quantum Mechanics
1. 3D Rotation of the frame (x,y,z) matrices
1.1. Around z-axis
We consider the rotation of the frame (x, y, z) to
the new one (x', y' z'). The coordinate x becomes
x', y becomes y' and z remains inchanged z = z'.
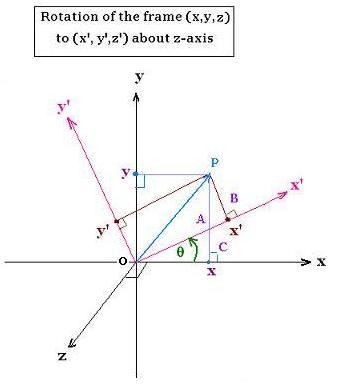 x' = oA + AB (1)
x/oA = oc/oA = cos θ then oA = x/cos θ
The angle (A,P,B) is equal to the angle θ
because the triangles oAC and aAB are similar.
Ax'/AP = AB/AP = sin θ.
We have also:
AP = y - AC = y - x tg θ. The relationship (1) becomes:
x' = x/cos θ + AP sin θ = x/cos θ + (y - x tg θ) sin θ =
x/cos θ + y sin θ - x sin2 θ/cos θ = y sin θ + x cosθ
Thus
x' = x cosθ + y sin θ
Now
y' = PB = AP cos θ = (y - x tg θ)cos θ =
y cos θ - x sin θ
x' = x cosθ + y sin θ
y' = - x sin θ + y cos θ
z' = z
The related matrix is:
x' = oA + AB (1)
x/oA = oc/oA = cos θ then oA = x/cos θ
The angle (A,P,B) is equal to the angle θ
because the triangles oAC and aAB are similar.
Ax'/AP = AB/AP = sin θ.
We have also:
AP = y - AC = y - x tg θ. The relationship (1) becomes:
x' = x/cos θ + AP sin θ = x/cos θ + (y - x tg θ) sin θ =
x/cos θ + y sin θ - x sin2 θ/cos θ = y sin θ + x cosθ
Thus
x' = x cosθ + y sin θ
Now
y' = PB = AP cos θ = (y - x tg θ)cos θ =
y cos θ - x sin θ
x' = x cosθ + y sin θ
y' = - x sin θ + y cos θ
z' = z
The related matrix is:
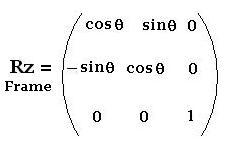
1.2. Around x-axis
In this case, y takes the place of x, and y the
place of z and x remains the same, we get then:
y' = y cosθ + z sin θ
z' = - y sin θ + z cos θ
x' = x
Or
x' = x
y' = y cosθ + z sin θ
z' = - y sin θ + z cos θ
The related matrix is:
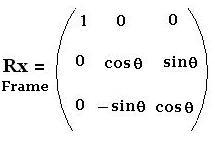
1.3. Around y-axis
In this case, y takes the place of x, and y the
place of z and x remains the same, we get then:
z' = z cosθ + x sin θ
x' = - z sin θ + x cos θ
y' = y
Or
x' = x cos θ - z sin θ
y' = y
z' = x sin θ + z cosθ
The related matrix is:
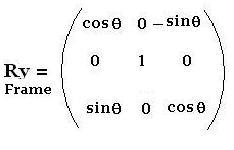
2. Vector position 3D Rotation matrices
2.1.. Around z-axis
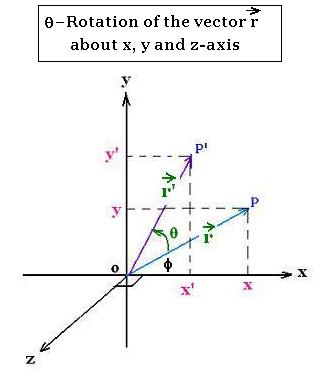 We have :
||r'|| = ||r|| = r
x = r cos φ and y = r sin φ.
x' = r' cos(φ + θ) = r cos (φ + θ) = r cos φ cosθ - r sinφ sin θ =
x cosθ - y sin θ
y' = r' sin(φ + θ) = r sin (φ + θ) = r sin φ cosθ + r cos φ sin θ =
y cosθ + x sin θ = x sin θ + y cosθ
z' = z
Therefore:
x' = x cosθ - y sin θ
y' = x sin θ + y cosθ
z' = z
The related matrix is:
We have :
||r'|| = ||r|| = r
x = r cos φ and y = r sin φ.
x' = r' cos(φ + θ) = r cos (φ + θ) = r cos φ cosθ - r sinφ sin θ =
x cosθ - y sin θ
y' = r' sin(φ + θ) = r sin (φ + θ) = r sin φ cosθ + r cos φ sin θ =
y cosθ + x sin θ = x sin θ + y cosθ
z' = z
Therefore:
x' = x cosθ - y sin θ
y' = x sin θ + y cosθ
z' = z
The related matrix is:
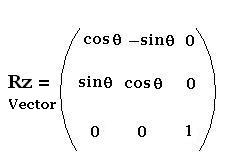
2.2. Around y-axis
z takes the place of x and x the place y, so:
z' = z cosθ - x sin θ
x' = z sin θ + x cosθ
y' = y
x' = x cosθ + z sin θ
y' = y
z' = - x sin θ + z cosθ
The related matrix is:
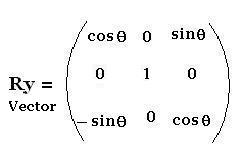
2.3. Around x-axis
y takes the place of x, and z the place pf y so:
y' = y cosθ - z sin θ
z' = y sin θ + z cosθ
x' = x
x' = x
y' = y cosθ - z sin θ
z' = y sin θ + z cosθ
The related matrix is:
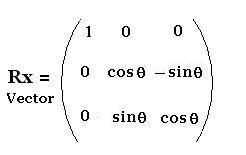
Remark: RFrame (θ) = RVector (- θ)
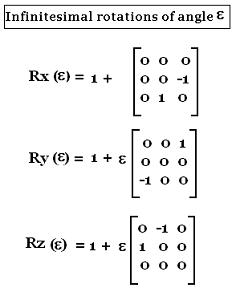
The related matrices rotating a vector by an
infinitesimal angle ε are:
3. Vector infinitesimal rotation
3.1 Infinitesimal translation
Let t(a) a linear translation that moves a vector r to
the vector r' by the vector "a". the magnitude of the
vector r does not change. We do not add vectors, but
translate a vector. We have r' = t(r) = r + a centred
at the origin O. Its magnitude doesn't change and remains
"r". But centred at the new origin "a", we have
r = r'(a) = r'(o) - a (as we translate the frame (o,r)).
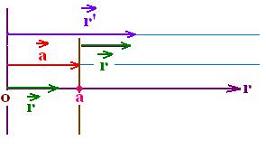 The operator translation T acts as follows:
T(a)(|ψ(x)>) = |ψ(x - a)>
It moves a wave function centred at the origin to
be centred at the point "a".
Writing the Taylor series in operator form yields:
ψ(x - a) = ψ(x) - a(d/dx) ψ(x) + (1/2!)a2 d2/dx2 ψ(x) + ...
That is:
T(a) ψ(x)> = [Σ (-a)n(1/n!)an dn/dxn ] ψ(x) =
exp {- a d/dx} ψ(x)
Then:
T(a) = exp {- a d/dx}
with p = - i ℏ d/dx, we obtain:
T(a) = exp {- ia p/ℏ}
T(a) = exp {- a d/dx}
T(a) = exp {- ia p/ℏ}
At the second order, we have the case of
an infinitesimal translation:
T(ε) = 1 - iεp/ℏ
The momentum operator p is seen as
the generator of translation.
The operator translation T acts as follows:
T(a)(|ψ(x)>) = |ψ(x - a)>
It moves a wave function centred at the origin to
be centred at the point "a".
Writing the Taylor series in operator form yields:
ψ(x - a) = ψ(x) - a(d/dx) ψ(x) + (1/2!)a2 d2/dx2 ψ(x) + ...
That is:
T(a) ψ(x)> = [Σ (-a)n(1/n!)an dn/dxn ] ψ(x) =
exp {- a d/dx} ψ(x)
Then:
T(a) = exp {- a d/dx}
with p = - i ℏ d/dx, we obtain:
T(a) = exp {- ia p/ℏ}
T(a) = exp {- a d/dx}
T(a) = exp {- ia p/ℏ}
At the second order, we have the case of
an infinitesimal translation:
T(ε) = 1 - iεp/ℏ
The momentum operator p is seen as
the generator of translation.
3.2 Infinitesimal rotation
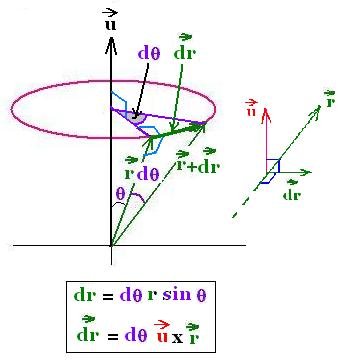 An infinitesimal rotation dθ rotates a vector
r to a vector r' = r + dr = r + dθ u x r.
As for a translation, this rotation lets the magnitude of
the vector r unchanged. The infinitesimal rotation
transforms the vector r to the vector r - dr at the
point of the end of the rotation dr. Therefore:
R(dθ) = exp {- i dr.p/ℏ} = exp {- i (dθ u x r).p/ℏ} =
exp {- i (dθ u.r x p/ℏ} = exp {- i (dθ u.L/ℏ}
u" is a unit vector, so: u.L = L.
R(dθ) = exp {- i (dθ L/ℏ}
L = r x p
L = r x p the orbital angular momentum. Indeed,
It is the generator of rotations.
R(θ) = exp {- i (Σdθ u.L/ℏ} =
exp {- i θ u.L/ℏ}
An infinitesimal rotation dθ rotates a vector
r to a vector r' = r + dr = r + dθ u x r.
As for a translation, this rotation lets the magnitude of
the vector r unchanged. The infinitesimal rotation
transforms the vector r to the vector r - dr at the
point of the end of the rotation dr. Therefore:
R(dθ) = exp {- i dr.p/ℏ} = exp {- i (dθ u x r).p/ℏ} =
exp {- i (dθ u.r x p/ℏ} = exp {- i (dθ u.L/ℏ}
u" is a unit vector, so: u.L = L.
R(dθ) = exp {- i (dθ L/ℏ}
L = r x p
L = r x p the orbital angular momentum. Indeed,
It is the generator of rotations.
R(θ) = exp {- i (Σdθ u.L/ℏ} =
exp {- i θ u.L/ℏ}
3.3 Example: Infinitesimal rotation about z-axis
A rotation of a vector r (x,y,z) about an
axis by an angle θ is equivalent to
a translation of its components. For
example, about z-axis (x,y,z) becomes (x',y',z'):
x' = x cosθ - y sin θ
y' = x sin θ + y cosθ
z' = z
For an infinitesimal rotation dθ, we have:
x' = r cos (θ + dθ) = x - y dθ
y' = r sin(θ + dθ) = x dθ + y
z' = z
Then:
R(z, dθ) = (x - y dθ, x dθ + y,0) =
T(- y dθ)(x) . T(+x dθ)(y) . T(0)(z) =
exp {- i(- y dθ) px/ℏ} . exp {- i x dθ py/ℏ} . exp {- i 0 pz/ℏ}
= exp {- i dθ/ℏ (- y px + x py)} = exp {- i dθLz} =
Where Lzis the z-component of the angular
momentum L.
3.3 Generalization of the Rotation Operator
Taking account of the spin S of the
system, we can generalize the orbital angular
momentum to the operator J that is, therefore,
defined as the generator of rotations for any
wave function of a quanum system.
R(dθ) = exp {- i dθ J/ℏ}
This expression of J can be used along with the properties
of a rotation (or infinitesimal rotation) to set
the properties of the J's such as commutations.
|
|