Quantum Mechanics
Schrodinger equation
Quantum Mechanics
Propagators : Pg
Quantum Simple Harmonic
Oscillator QSHO
Quantum Mechanics
Simulation With GNU Octave
© The scientific sentence. 2010
|
|
Many-electron atom:
Identical and non-interacting particles
1. Two non-identical and non-interacting particles:
Consider a system that contain two identical particles of mass m as Helium
atom. The instantaneous state of the system is: ψ(r1, r2,t) that we
can, if these particles are non identical and non-interacting ,
express by:
ψ(r1,r2,t) = ψ(r1,t) ψ(r2,t)
With
ψE(r1, r2) =
ψE1(r1) ψE2(r2), and
E = E1 + E2
|ψ(r1,r2,t)|2 dr1 dr2 = the probability of finding a first
particle between r1 and r1 + dr1 and the second particle
between r2 and r2 + dr2, at a time t.
What about if they are identical and non-interacting particles
2. Two identical and non-interacting particles:
If the two particles of the system are identical we can write
that the probability to find a first particle, at a time t, at a position
between r and r + dr is the same for the second particle, because the two
particles are indistinguishable.
In other words, since the two particle are identical, the probability
to find a first particle between r1 and r1 + dr1 and the second particle
between r2 and r2 + dr2 is equal to the probability of finding the
first particle between r2 and r2 + dr2 and the second particle
between r1 and r1 + dr1
2.1 Symmetry of of the system's wave-function
The first probability is |ψ(r1,r2,t)|2dr1 dr2, and the second
is |ψ(r2,r1,t)|2dr2 dr2. Therefore:
|ψ(r1,r2,t)|2 = |ψ(r2,r1,t)|2
Hence
ψ(r1,r2,t) = ε ψ(r2,r1,t) exp {i θ}
With ε = ± 1.
We conclude that for a system that containing
two non-interacting identical particles, under label interchange, the wave-function
of each one is either:
symmetric, that is:
ψ(r1,r2,t) = + ψ(r2,r1,t)
or
anti-symmetric, that is:
ψ(r1,r2,t) = - ψ(r2,r1,t)
Any particles that have a symmetric wave-function obey Bose-Einstein Statistics, and
are called bosons (s photons) . The particles that have an anti-symmetric wave-function obey
Fermi-Dirac Statistics, and are called fermions (as electrons and protons).
For a system of two particles, the wave-function ψ(r2,r1,t) that
describe this system is no longer just the product of its
components ψ(r1,t) and ψ(r2,t) of each particle. It is
a linear combination of this product:
ψ(r2,r1,t) = c1 ψ(r1,t) ψ(r2,t) + c2 ψ(r2,t) ψ(r1,t)
With
ψ(r1,r2,t) = ψ(r1,r2) exp{- iE/ħ}
ψ(r1,t) = ψ(r1) exp{- iEa/ħ}
ψ(r2,t) = ψ(r2) exp{- iEb/ħ}
With E = Ea + Eb
That gives with the stationary wave-function:
ψ(r2,r1) = c1 ψ(r1) ψ(r2) + c2 ψ(r2) ψ(r1)
(1)
For the stationary state, at the position r1, we can have
either the particle 1 with energy Ea, or the particle 2
with energy Eb, and at the position r2, we have
either the particle 1 with energy Ea, or the particle 2
with energy Eb. Indeed, since the particles are identical,
we cannot be sure which particle has energy Ea, and which has
energy Eb. We say one particle has energy Ea, and the other Eb.
That is, we have either:
ψ(r1,Ea) ψ(r2,Eb) or ψ(r1,Eb) ψ(r1,Ea)
The above equation is, instead, written as:
ψ(r2,r1,E) = c1 ψ(r1,Ea) ψ(r2,Eb) + c2 ψ(r1,Eb) ψ(r2,Ea)
ψ(r2,r1,E) = c1 ψ(r1,Ea) ψ(r2,Eb) + c2 ψ(r1,Eb) ψ(r2,Ea)
(2)
The normalisation of this function is written as:
1 = |ψ(r1,r2)|2 = <ψ*(r1,r2)|ψ(r1,r2)>
= ∫ dr1 dr2 ψ*(r1,r2)ψ(r1,r2)
from - ∞ to + ∞
= < c1*ψ*(r1,Ea) ψ(r2,Eb) + c2* ψ*(r2) ψ*(r2,Eb) | c1 ψ(r1) ψ(r2) + c2 ψ(r2) ψ(r1) >
=
< c1* c1 ψ*(r1,Ea) ψ*(r2,Eb) |
ψ(r1,Ea) ψ(r2,Eb)> +
< c1* c2 ψ*(r1,Ea) ψ*(r2,Eb) |
ψ(r1,Eb) ψ(r2,Ea) > +
< c2* c1 ψ*(r1,Eb) ψ*(r2,Ea) |
ψ(r1,Ea) ψ(r2,Eb)> +
< c2* c2 ψ*(r1,Eb) ψ*(r2,Ea) |
c2 ψ(r1,Eb) ψ(r2,Ea)>
The four wave-functions ψ(ri,Ej) (i = 1, 2, and j = a, b)
are orthogonal. It remains:
|c1|2 + |c2|2 = 1
The outcomes are equally likely to occur, then:
|c1|2 = |c2|2
Therefore:
|c1|2 = 1/2 , and |c1|2 = ± 1/(2)1/2
The equality (2) becomes:
ψ(r2,r1,E) = 1/(2)1/2 [ψ(r1,Ea) ψ(r2,Eb) &plusmin; ψ(r1,Eb) ψ(r2,Ea)]
+ for the bosons and - for the fermions.
Therefore:
For a system of two identical and non-interacting fermions with an antisymmetric wave-function:
ψ(r1,r2,t) = - ψ(r2,r1,t)
The stationary wave-function of the whole system is:
ψ(r1,r2,E) = 1/(2)1/2 [ψ(r1,Ea) ψ(r2,Eb) - ψ(r1,Eb) ψ(r2,Ea)]
For a system of two identical and non-interacting bosons with an antisymmetric wave-function:
ψ(r1,r2,t) = +ψ(r2,r1,t)
The stationary wave-function of the whole system is:
ψ(r1,r2,E) = 1/(2)1/2 [ψ(r1,Ea) ψ(r2,Eb) + ψ(r1,Eb) ψ(r2,Ea)]
For a system of two non-identical (distinguishable) and non-interacting particles,
the stationary wave-function of the system is simply:
ψ(r1,r2,E) = ψ(r1,Ea) ψ(r2,Eb)
2.2 Pauli exclusion principle
If Ea = Eb for the fermions, then their total wave-function ψ(r2,r1,E)
becomes zero. That is, there is no state!. We must then exclude this
possibility and say that it is impossible for the two fermions
to occupy the same single-particle stationary state.
That is the Pauli exclusion principle.
3. Non-interacting
and identical multi-particles system
The symmetry of a wave-function of a system with two non-interacting
and identical particles can be extended to systems containing more than two identical particles. For a system containing N identical and non-interacting fermions, the anti-symmetric stationary wave-function of the system is written as the
Slater determinant:
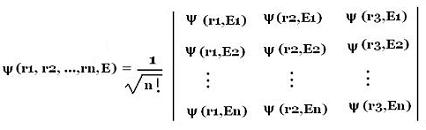
|
|