Quantum Mechanics
Schrodinger equation
Quantum Mechanics
Propagators : Pg
Quantum Simple Harmonic
Oscillator QSHO
Quantum Mechanics
Simulation With GNU Octave
© The scientific sentence. 2010
|
| Tensor operators
1. Definition of a rotated operator
Let's write the rotation operator as U(R). This operator
rotates a ket |ψ> to the ket |ψ'>.
If A is any operator, the rotated operator A' must be
unchanged with respect to its expectations before and
after rotation. That is:
<ψ'|A'|ψ'> = <ψ|A|ψ>.
We have then:
<ψ|A|ψ> = <ψ|U+(R)A'U(R)ψ>. Therefore:
A = U+(R)A'U(R) or A' = U(R)AU+.
Hence:
The rotated operator of the operator A is A' = U(R)AU+,
where U(R) is the rotation operator.
2. Scalar Operators
A scalar operator is invariant under rotations. That is:
K = U(R)KU+ under any rotation operator U(R).
This definition implies that U(R) and K commute: [U(R),K] = 0.
The scalar operator commutes with any rotation operator U(R);
in particular with the rotation operator R(θ) = exp {- i θ J/ħ}
or its infinitesimal rotation operator: R(dθ) = 1 - idθJ/ħ;
hence, it commutes with the angular momentum J.
We have then a new definition:
A scalar operator K commutes with the
angular momentum J if
[J, K] = 0
3. Vector Operators
In three-dimensional Euclidean space, a vector is
defined as a set of three numbers. Under rotation,
these numbers are transformed according certain rules.
Similarly, in quantum mechanics, we define a vector operator
as a vector of operators (that is, a collection of
three operators) with certain transformation
properties under rotations.
For its definition,a vector operator "V" must have
its expectation rotated according the definition of
the rotation of any ordinary vector. That is:
If |ψ'> is the rotated state of
the original one |ψ>, we have:
R <ψ|V|ψ> = <ψ'|V|ψ'>
In components form:
V'i = <ψ'|Vi|ψ'> = Σ (j) Rij <ψ|Vj
Using |ψ'> = U(R) |ψ>,, the definition becomes:
R <ψ|V|ψ> = <ψU(R)+|V|U(R)ψ>. So
R V = U(R)+|V|U(R), or R-1 V = U(R)VU+(R)
(the adjoint of the rotation R is equal to its inverse R-1)
The definition of a vector operator becomes:
R V = U+(R)VU(R)
For an infinitesimal rotation about the z-axis
by an angle ε, we have:
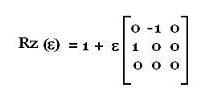 V'i = (V'x , V'y , V'z) = Rz(ε) (Vx , Vy , Vz)
= (Vx - εVy, Vy + εVx, Vz)
Using the expression of the rotation operator
U(R) = 1 - iεJz/ħ, to find:
U+(R)Vi)U(R) = (1 + iεJz/ħ)Vi)(1 - iεJz/ħ) =
Vi + (iε/ħ)[Jz, Vi]
Therefore:
i[Jz, Vx] = - ħ Vy
i[Jz, Vy] = - ħ Vx
The cyclic equivalents give the related commutation
relations of the components of any vector operator V:
[Vi, Jj] = iħεijkVk
[Vi, Jj] = iħεijkVk
εijk is the Levi-Civita element:
εijk =
+1 for even permutations: 123,231,312
-1 for odd permutations: 132,213,321
0 otherwise
V'i = (V'x , V'y , V'z) = Rz(ε) (Vx , Vy , Vz)
= (Vx - εVy, Vy + εVx, Vz)
Using the expression of the rotation operator
U(R) = 1 - iεJz/ħ, to find:
U+(R)Vi)U(R) = (1 + iεJz/ħ)Vi)(1 - iεJz/ħ) =
Vi + (iε/ħ)[Jz, Vi]
Therefore:
i[Jz, Vx] = - ħ Vy
i[Jz, Vy] = - ħ Vx
The cyclic equivalents give the related commutation
relations of the components of any vector operator V:
[Vi, Jj] = iħεijkVk
[Vi, Jj] = iħεijkVk
εijk is the Levi-Civita element:
εijk =
+1 for even permutations: 123,231,312
-1 for odd permutations: 132,213,321
0 otherwise
4. Tensor Operators
A tensor operator is a matrix of operators. That is each element
of the matrix is an operator. For example, if we have:
A = (A1, A2, A3), and
B = (B1, B2, B3); we
can construct a 3x3 tensor Tij = AiBj.
This is the case of a rank-2 tensor.
Before rotation, we have Vi and Wj, then
a tensor Tij. After rotation we have T'ij.
We are going to express the matrix elements of T', that is
T'ij function of Tij.
We have already V'i = Σ(k) Rik Vk
W'j = Σ(l) Rjl Wl
Then:
T' = V' ⊗ W' and T'ij = V'i ⊗ W'j = Σ(k) Rik Vk Σ(l) Rjl Wl =
Σ(k) Σ(l) Rik Rjl VkWl
ViWj = Tij, then:
T'ij = Σ(k)Σ(l) Rik Rjl Tkl
Therefore:
T'ij = U+(R)TijU(R) = Σ(k)Σ(l) Rik Rjl Tkl
Since the suffixes i, j, ... refer to Cartesian axes. Tensors
written this way are called Cartesian tensors. The
number of suffixes in "T" is the rank of the Cartesian
tensor (Tij has the rank 2). The rank n
tensor has 3n components. A rank 3 Cartesian tensor
is transformed as:
T'ijk = Σ(l) Σ(m) Σ(n) Ril Rjm Rkn Tlmn,
having 27 components.
Now we will represent a Cartesian tensor in spherical coordinates
and talk about spherical tensor
4.1.Spherical Vector
The angular momentum eigenkets |l,m> = Ylm(θ,φ),
called spherical harmonics can be expressed for l = 1:
|1,0> = Y10(θ,φ) = [3/4π]1 (z/r)
|1,-1> = Y1-1(θ,φ) = +[3/4π]1(x - i y)/21/2 r
|1,1> = Y11(θ,φ) = - [3/4π]1(x + i y)/21/2 r
x, y , and z are considered position operators.
r = (x, y, z) is a vector operator that will be transformed
under rotation U(R) to the vector operator r' by rotating
the eigenstates |l,m>
The eigenstates operators |l,m> will be considered as
eigenstates operators |j,m>.
|j=1,m> → U(R(θ))|j=1,m> = exp {-iθJ/ħ} |j=1,m> =
Σ(m') <j=1,m'|exp {-iθJ/ħ}|j=1,m> |j=1 m'>
with:
D(j)m'm(Rθ)) = <j,m'|exp {-iθJ/ħ)}|j,m>
We have:
|j=1,m> → U(R(θ))|j=1,m>Σ(m') D(j=1)m'm(Rθ) |j=1 m'>
Therefore:
If (Vx,Vy,Vz) are the operators components of
a vector operator V in Cartesian coordinates,
in spherical coordinates, they become:
V11, V-11, V01, with:
V-11 = +(Vx - iVy)/[2]1/2
V+11 = -(Vx + iVy)/[2]1/2
V01 = Vz
To work with the same notation T, we write:
T-11 = +(Vx - iVy)/[2]1/2
T+11 = -(Vx + iVy)/[2]1/2
T01 = Vz
These components are denoted Tq1.
The definition :
V'i = Σ (j) Rij |Vj
becomes:
T'q = Σ(q') Rqq' Tq', or
T'q1 = Σ(q') Rqq' Tq'1
More generally, a rank k vector operator having 2k+1
(q varies from = k to +k) components is written as
Tqk. If k = 2, we have a
spherical tensor.
4.2.Spherical Tensor
We ca generalize the latter result to define a spherical
tensor of rank k as a set of 2k + 1 operators:
Tqk; q = -k, ...+k, which
under rotation R, they are transformed with the
matrix of 2j+1 elements D(k)mm' = <j,m|exp{-iθJ/ħ|jm>} .
That is:
U(R)TqkU+(R) = Σ(q) D(k)q'q'Tq'k
Let's recall:
D(k)mm' = <j,m|exp{-iθJ/ħ|jm>}
U(R)TqkU+(R) = Σ(q) D(k)q'q'Tq'k
Using the expression of the infinitesimal rotation
operator U(R(dθ)) = 1 - i εJ/ħ, we find the
commutation relations:
[J+, Tqk] = +ħ [(k-q)(k+q+1)]1/2 Tq+1k
[J-, Tqk] = -ħ [(k+q)(k-q+1)]1/2 Tq-1k
[Jz, Tqk] = ħ q Tqk
|
|