1. Definitions

On rappelle que le but de la régulation est de minimiser l'écart entre une grandeur mesurée (PV) et une consigne (SP) en agissant sur une grandeur de commande (Out%).

Une perturbation est une grandeur d'entrée pour le régulateur. Elle a un effet indésirable sur le fonctionnement du procédé. Elle peut être mesurable ou aléatoire. L'exemple d'une perturbation mesurée est une augmentation brusque de la variable du procédé PV, due à un changement brusqye de débit, ou de la consigne SP.

Un système peut être dans deux types de régimes :
- Permanent ou stabilisé ou stationnaire, si ses entrées et sorties sont des constantes, principalemenr le débit.
- Transitoire si ces entrées et/ou sorties évoluent avec le temps.

Le gain (généralement choisi et fixé dans le cntrolleur) est le moyen d'intensifier ou réduire l'action de de la vanne de régulation. Pour le controlleur, c'est un moyen de multiplication ou division. On le représente par G dans la formule de la commande: Out% = G (SP - PV) + Bias. On le note aussi K_p ou 1/PF, pour proportionnal factor, pour ecrire: Out% = (SP - PV)/PF + Bias.

Si par par une perturbation d'ouverture de la vanne de décharge (de soutitrage), le PV descend. Un écart d'une valeur "e" survient donc entre PV et SP. cette variation de niveau arrive au régulateur en terme de M% = SP - PV. Le régulateur agit donc en conséquence pour reduire cet écart. Il y a trois sortes d'action donc trois modes de régulation pour contrer la perturbation.

1.Mode proportionnel

Le régulateur répond à la variation de niveau "e" d'une façon proportionnelle. C'est à dire si l'écart est de 2 cm, le controlleur de gain G (= 17% par exemple), enverra un signal Out% de 17 x 2 = 34% vers le convertisseur puis vers la vanne de régulation; qui s'ouvrira proportionnellement à l'écart "e" en augmentant le débit. Ainsi, l'écart "e" se réduit mais ne s'élimine pas complètement; il se ramène à une erreur residuelle dite erreur statique. Cette valeur de commande Out% n'est jamais parfaite et le PV ne retrouvera jamais le SP; l'erreur statique résiduelle reste et persiste. Ceci est due au fait que le gain est soit trop fort, soit trop faible.

Ainsi cette action:
- Permet de corriger les effets d'une perturbation,
- Destabilise le système quand on augmente le gain,
- Mais elle n'annule pas l'erreur.

Pour ramener les choses comme avant de telle sorte que SP = PV exactement, on utilise un autre mode de régulation dit mode integral.

2.Mode integral

Le mode integral n'utilise pas le gain comme le fait le mode proportionnel. Il peut juste être amplifié par un certain facteur K_i. Mais il tient compte du temps qui s'ecoule au fur et à mesure que la correction progresse, c'est à dire durant la progression de la réduction de l'ecart e = SP - PV. Durant un intervalle de temps dt, un signal partiel donnera une correction partielle produit de e par dt, soit e x dt. Si la correction totale durera un temps T, elle portera sur la somme de l'écart "e" pendant T, soit e x T . En fait, la correction est la somme de toutes les corrections élementaires e x dt durant le temps T. On ecrit: Out% = correction totale = e x T = ?e dt (t: 0 ? T).
Exemple:
Si L'écart e = 30 cm dans le reservoir et représente 7% dans le régulateur; dt est égal à 1/10 seconde, et T = 5 secondes; la valeur de la commande à partir du régulateur est donc égale 50 fois e x (1/10); soit , Out% = 5 x 7% = 35%.

Si le mode integral travaille tous seul, la valeur de son signal de commande correspondant à Out% va pouvoir permettre à la vanne de régulation de:
- S'ouvrir jusqu'à ce que le PV s'pproche de SP (ce qui ce fait par le mode proportionnel); plus
- De continuer à s'ouvrir pour faire ramener exactement le PV au SP; c'est à dire annuler complètement l'écart e = SP - PV. À ce niveau, les valeurs de la commande Out% oscille pendant une période de temps pour s'amortir par la suite. Finalement l'erreur est annulée.

L'action integrale:
- Corrige les effets d'une perturbation,
- Annule l'erreur statique,
- Introduit un dépassement,
- Mais elle n'est pas très rapide.

Pour faire les chose plus rapidement, on utilise aun dernier mode dit mode dérivé

3.Mode dérivé

Lorsqu'une variation de l'écart apparait, le mode dérivé agit immédiatement sous forme de signal Out% = K_ede/dt, c'est à dire une variation de l'ecart en fonction du temps, K_e est just un facteur multiplicatif d'amplification.

L'action dérivée:
- Accélère la correction,
- Stabilise plus rapidement le système,
- Mais n'annule pas l'erreur statique et est sensible aux vibrations.

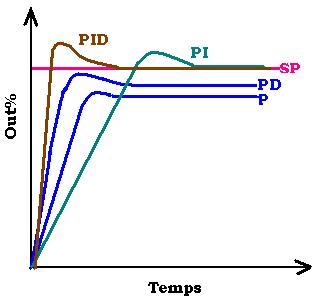
4.Combinaison des modes: Le mode PID

On peut faire des combinaisons des trois modes comme le mode PD, PI ou PID. Le plus courant employé est le PID: Proportional Integral Derivative, de par le fait qu'il rammeble les avantages des trois modes. On aussi les associer en série ou en parallèle
Pour le PID série, le Out% prend l'expression suivante:

Out% = K_p e + K_i ? e(t)dt + K_d de(t)/dt
où: K_p est le gain proportionnel, K_i la constante de l'intégrale et K_d celle de la dérivée.

5. Autre expression du signal de commande en mode PID

Action PI:

La constante K_i de l'action integrale est proportionnelle à l'action proportionnelle P:
K_i = K_p/T_i
T_i est le temps de l'action integrale exprimé en minutes (min). Il peut être fixé sur le régulateur.
Si l'écart e est constant, e variant de 0 à T_i; on peut ecrire:
K_i? edt = K_i x e x (T_i - 0) = e x T_i& x K_i = K_p. Ainsi, le temps T_i correspond au temps pour lequel le mode integral est égal au mode proportionnel. Au temps 2T_i, le mode I ( integral) fera le double de celui de P (proportionnel). Si T_i = 0.25 minutes, en 5 minutes, le mode I aurait répété 20 fois le mode P. Autrement dit pour l'action I, le temps T_i represente le temps de répetition du mode P. T_i est donc plutôt exprimé en temps par répétition. 1/T_i est alors le nombre de répétitions par minute.

Action PD: Sans l'action dérivée D, le signal de sortie (de P seulement) aurait la même valeur qu,avec le mode D mais Ti minutes plus tard. Exemple: Ti = 1.5 min et Out% (valeur de sortie) = 45%. Cette valeur de sortie de 45% est atteinte au bout de 1,5 min avec P seulement. Mais avec le mode D, elle serait déjà atteinte 1.5 minutes à l'avance. Le coefficient de l'action dérivée Kd est aussi proportionnel à Kp: Kd = Kp x Td

Action PID:

Finalement l'exression du signal de commande incluant les 3 modes : propoportionnel, integrale et dérivée peut s'ecrire:

Out% = K_p [e + (1/T_i) ? e(t) dt + T_d de(t)/dt]

On peut ajouter dans cette expression le terme Bias, pour montrer que lorsque l'ecart "e" est nul, la valeur de sortie (donc de la vanne dans le cas d'un réservoir) est à Bias%. Ainsi:

Out% = K_p [e + (1/T_i) ? e(t) dt + T_d de(t)/dt] + Bias

Avec le mode PID, c'est vite fait, bien fait.