Probability & statistics

1. Bernoulli trials

A Bernoulli process is a sequence of repeated trials 
of an experiment in which:
- Each trial has two possible outcomes E and E (success or failure)
- The trials are indepenedent
- The probability p(E) of an event E is the same for each trial

Let's recall that a trial is independent means that it does 
not depend on any other trials; that is the outcome of one trial 
does not influence the outcome of any other trial.

If p(E) is the probability of succes; then, according to the complement 
rule q = 1 - p(E) is the probability of failure.

The main purpose of the Bernoulli trials is to determine 
the probability that an event E occurs exactly "r" times among 
a series of "n" trials of a random experiment.

We can solve a problem by two approches:
1. Using a stochastic diagram

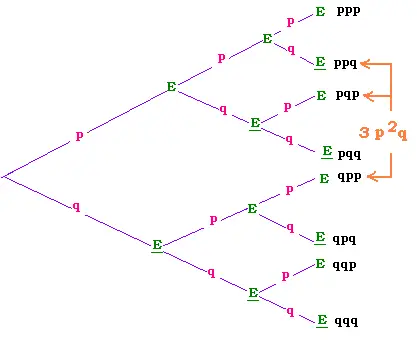The probabilty to have "success" twice among three trials 
is ppq or p2q. it occurs three times. We ad them 
to have the total probability, that gives 3 p2q
(aal of the branches of the tree are mutually exclusive).
As we have seen the number three in 3 p2q is 
a numer of combinations, that is C(2,3)=3. Finally, the  
probability to have success twice is C(3,2)p2q.

2. Using the Binomial formula
1 = (p+q)N = = ∑ C(n,N)pnqN-n	[n: 0 → N]
in which each term of the series represents the probability to 
get "success" "n" times among N trials.

The collection {p(m,n), m = 1,2,3 ... n} forms a probability 
distribution called the binomial distribution.