We have seen that:
The Gaussian distribution:
P(x) = 1/σ(2π)1/2 exp {- (x - μ)2/2σ2}
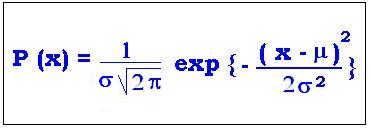
2. Normal distribution is a density probability
The normal distribution, or Gaussian distribution
pμ(x) is a density probability, because it
satisies the two following criteria:
- 1. p(x) ≥ 0, and
- 2. &int p(x) dx = 1 [x: - ∞ → + ∞]
-1. p(x) is ≥ 0 as we can see in its graph at the bottom,
-2. &int p(x) dx ≟ 1
&int p(x) dx [x: - ∞ → + ∞]
= ∫ (1/2πμ)1/2 exp {- (x - μ)2/2μ} dx
= (1/2πμ)1/2 ∫ exp {- (x - μ)2/2μ} dx
Let's write:
y2 = (x - μ)2/2μ or
y = (x - μ)/(2μ)1/2
Then dy = dx /(2μ)1/2
I = ∫ exp {- (x - μ)2/2μ} dx
= (2μ)1/2 ∫ exp {- y2} dy
J = ∫ exp {- y2} dy
J2 = ∫∫ exp {- x2}dx ∫ exp {- y2} dy
= ∫ ∫ exp {- (x2 + y2 )}dxdy
= ∫ ∫ exp {- r2}r dr dθ
[r: 0 → + ∞ and θ 0 → π]
= π ∫ exp {- r2}r dr
= (π/2) ∫ exp {- r2} 2r dr
= 2 exp {- r2}
[r: 0 → + ∞]
= π
Then:
J = π1/2
I = (2μ)1/2 π1/2 = (2 π μ)1/2
&int p(x) dx = (1/2πμ)1/2 I =
= (1/2πμ)1/2 (2 π μ)1/2 = 1
The total area under the curve is 1.00:
∫(1/2πμ)1/2 exp {- (x - μ)2/2μ} dx = 1
We can also verify that:
∫ x p(x) dx = μ [x: - ∞ → + ∞] , and
∫ (x - μ)2 p(x) dx = σ2 [x: - ∞ → + ∞ ]
2. Some properties of the normal distribution
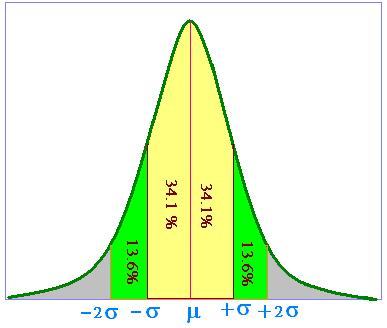
The area under the curve between any two values is a probability;
that is the chance to find a value between these two values.
P(a < x <: b) = ∫ P(x) dx [x: a → b ]
with :
x = μ + 0 x σ , have:
P(x) = (1/2πμ)1/2
x = μ + 1 x σ , have:
P(x) = (1/2πμ)1/2 exp{- 1/2} = 60.6% (1/2πμ)1/2
x = μ + 2 σ , have:
P(x) = (1/2πμ)1/2 exp{- 2} = 13.5% (1/2πμ)1/2
x = μ + 3 σ , have:
P(x) = (1/2πμ)1/2 exp{- 9/2} = 1.1% (1/2πμ)1/2
- The total area under the curve is 1.00
The related empirical rule shows:
- Approximately 68% (∫p(x)dx [- σ → + σ ]) of values
lies within 1 standard deviation of the mean,
- About 95% (∫p(x)dx [- 2σ → + 2σ ]) of the values
are within two standard deviations,and
- About 99.7% (∫p(x)dx [- 3σ → + 3σ ])
lie within three standard deviations.
3. Standard rormal distribution
The Standard normal distribution stands on 0.
That is the mean μ is zero. The standard deviation σ = 1.
Its expression is:
The Standard Normal Distribution:
P(x) = 1/(2π)1/2 exp {- x2/2}