Probability
1. Poisson distribution
If the probability of one success is p; the probabily to get exactly
n success among N trials is:
P(n/N) = C(n,N)pnqN-n = [N!/n!(N-n)!] pnqN-n (1)
N!/(N-n)! = N x (N-1) x (N-2) x ... x (N- n+2) x (N - n+1) (2)
We define the parent parameter λ as:
λ = N x p
Where N is the number of trials, and p is the parent probability
to get success.
The expression (1) becomes:
P(n/N) = [N x (N-1) x (N-2) x ... x (N-n+2) x (N-n+1)/n!] (λ/N)n(1 - λ/N)N-n
= [N x (N-1) x (N-2) x ... x (N-n+2) x (N-n+1)/Nn] x
[λn/n!] x (1 - λ/N)N x (1 - λ/N)-n (3)
Now if N is large, the probability P(n/N) becomes:
pλ(n) = lim p(n/N) when n → ∞
pλ(n) = 1 x [λn/n!] x (1 - λ/N)N x 1 (4)
Using Taylor Series:
ex = 1 + x + x2/2! + x3/3! +... (T1)
(1 + x)n = 1 + nx + n(n - 1)/2! x2 + ... (T2)
we have respectively:
e- λ = 1 - λ + λ2/2! + ... (T11)
(1 - λ/N)N = 1 - λ + N(N - 1)/2!N2 λ2 + ... (T22)
When N → ∞ N(N - 1)/N2 → 1 ; the relationship (T22) becomes:
(1 - λ/N)N = 1 - λ + λ2/2! + ...
That is the relationship (T11)
Thus,
(1 - λ/N)N → e- λ
Finally, the relationship (4) becomes:
pλ(n) = [λn/n!] x e- λ
pλ(n) = λn e- λ/n!
More generally,
If we define the parent parameter λ as:
λ = N x p; where N is a large number of trials,
and p is the parent probability to get one success
(one event E); the probability of observing X = x;
where X is the random variable, a disctete value
that describes the number of times a given outcome
occurs is:
p(X = x) = λx e- λ/x!
The Poisson distribution is a discrete distribution that characterizes
the occurence of rare events. It is associated with counting experiments;
such as radioactive decay.
The parent probability p is associated with one (success)
outcome E, we can then write p = E(X)/N, where E(X) is the
expected value for the random variable X related to the
event E. The relationship λ = N x p becomes:
λ = E(X)
Using again the Taylor seriess:
ex = 1 + x + x2/2! + x3/3! +... = ∑ xn/n! (T1)
we sum the formula pλ(n) = λn e- λ/n!
to obtain:
∑pλ(n) = ∑λn e- λ/n!
= e- λ ∑λn/n! = e- λ eλ = 1
2. Poisson distribution Expectation value and variance
2.1. Expectation value
The expaectation value or mean for the Poisson distribution is:
E(x) = μ = ∑ x Po(x) [x: 0 → +∞]
= ∑ x μxe- μ/x! [x: 0 → +& infin;]
= e- μ ∑ μx/(x - 1)! [x: 1 →+ ∞]
= e- μ ∑ μx+1/x! [x: 0 → + ∞]
= e- μ μ ∑ μx/x! [x: 0 → + ∞]
According to the expansion:
eζ = ∑ ζx/x! [x: 0 → + ∞]
It follows:
E(x) = e- μ μ eμ = μ
Poisson distribution: Po(x) = μxe- μ/x!
Expectation = E(x) = μ
2.2. Variance
The variance of the Poisson distribution is:
σ2 = ∑ (x - μ)2 Po(x) [x: - ∞ → + ∞]
or
σ2 = ∑ (x - μ)2 Po(x) [x: 0 → + n]
for a large number n of measurements of x.
We have:
σ2 = ∑ x2 Po(x) - 2 μ ∑ x Po(x) + ∑ x2 Po(x)
= ∑ x2 Po(x) - 2 μ2 + ∑2
= ∑ x2 Po(x) - μ2
with x2 = x(x - 1) + x,
σ2 = ∑ (x(x - 1) + x) Po(x) - μ2
= ∑ (x(x - 1)) Po(x) + μ - μ2
= ∑ μxe- μ/(x - 2)!) + μ - μ2
= μ2 ∑ μx - 2e- μ/(x - 2)!) + μ - μ2
= μ2 ∑ μx - 2e- μ/(x - 2)!) + μ - μ2 [x: 2 → + n]
According to the expansion:
eζ = ∑ ζx/x! [x: 0 → + ∞]
It follows:
∑ μx - 2/(x - 2)!) [x: 2 → + n]
= ∑ μx /x! = eμ [x: 0 → + ∞]
Then:
σ2 = μ2 e+μ e-μ + μ - μ2 = μ
Poisson distribution: Po(x) = μxe- μ/x!
Variance = σ2 = μ
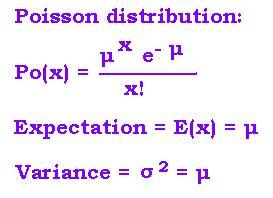
|