1. Equation of state
There are some and only some variables that govern the state of
a system. If we take a certain quantity of gas (then the number n of moles is fixed) in a certain container of
fixed size (then the volume V of the gas is fixed) and maintain this gas at a constant temperature T; experimentally, we find that the pressure P that the gas exerts in the container is determined. The variables P, V, n and T are called variables of state. The related relationship between these variables is called The equation of state .
For an ideal gas; the equation of state is: PV = nRT. (1.1)
This equation is known as the Boyle's law, where R is the universal gas constat; R = 8.31 J/mol/K.
Note that the temperature T is expressed on the Kelvin scale, and the ideal gas equation of state is obeyed by a dilute gas, that is a real gas whose pressure is low and whose temperature is not too low.
2. The P-V diagram
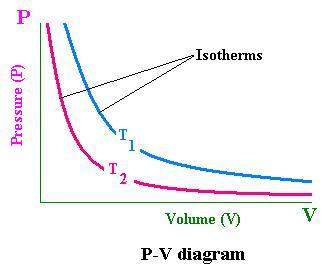With the equation of state; we can determine the value of one variable in terms of the others. If we fix the amount of gas (n remains fixed); for convenience, we choose P and V to be independent variables that allow us to have the value of the temperature T. in this case, the values of P and V determine the state of the gas. We represent the state of a system in a P-V diagram for any given temperature that is an isotherm.
Each point of the P-V diagram represents a state of the system. Holding T constant, we have a set of points related to an isotherm.
3. Heat and Temperature
Let's recall that heat is defined as the energy transferred between a system and its surroundings due to the temperature difference between them. The temperature of a system increases when adding heat to it. for instance, as heat is transferred to water from the surrounding (a burner), the temperature of water increases (on average the molecules move faster)to reach the boiling point. At this point, the temperature of water no longer changes. The added heat causes changing in phase from liquid to vapor (the interations between molecules decreases) without any chage in temperature.
Supposing that there is not yet a phase change and the pressure is fixed; for small temperature changes, Experiments show that the amount of heat added is proportional both to the temperature change and to the mass of the system. The related relationship can be written as the following equation:
dQ = mcpdT (3.1)
cp is a quantity characteristic of a substance and is called the specific heat capacity at constant pressure. When the volume is kept constatnt, we deal with cv.
For water, cp = 4.18 kJ/kg/K.
The specific heat cp is a function of temperature; but for small temperature changes cp is considered independent of temperature. In this case the equation (3.1) becomes:
Q = mcpΔT (3.2)
Q is the energy transferred and ΔT is the associated change in temperature.
4. Molar heat capacity
In the equations (3.1) and (3.2), we can express the mass of the substance in terms of its number of moles "n". Using the relationship m = nM, where M is the mass of a mole ( or gram molecular weight), we get for the equation (3.1), by writing Mcp = Cp:
dQ = nCpdT
Cp is called the molar heat capacity. Its SI unit is J/mol/K. When we consider a process with contant volume, we will deal with CV.
5. The calorie
The calorie (cal) is the unit of energy standing for the amount of heat required to raise the temperature of 1 g of water by 1 C0. The specific heat of water is thus cp = 1 cal./g/C0. The calorie is now defined as follows:
1 cal = 4.186 J
Another unit of heat is used, the Btu ( British thermal unit). It is equal to the amount of heat required to raise 1 lb( 1 libra = 0.4536 kg) of water by 1F0. Its equivalent is:
1 Btu = 1055 J
6. The latent heat
It involves the change in phase. At atmospheric pressure, and at the boiling point of water (100 C0), eventhough the temperature remains constant, heat is required to maintain the change in phase liquid-vapor. This necessary heat is called latent heat L. In this case, L is denoted Lv regarding the latent heat of vaporization. In the case of solid-liquid phase change, we have Lf standing for the latent heat of fusion.
The SI unit of latent heat is J/kg. For water, Lf = 0.335 MJ/kg and Lv = 2.260 MJ/kg. M stands for Mega = 106.
7. Work in Thermodynamics
Heat transferred between a system and its surrounding is a sort of energy. Another kind of energy is the work done by a system on its surrounding. When we boil water, we tranfer energy (heat) from the burner of a stove to a pot of water place on it; the result is an increase in temperature. If the lid on the pot is lifted because of the pressure inside the pot, water did a mechanical work on it. The burner, water (in the pot) and the lid changed energy between eath other. We call system one of them and the surrounding the other in order to have positive the work done.
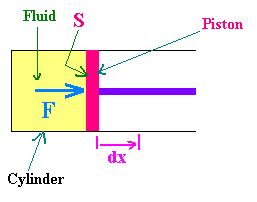
The work done by the system (fluid) is positive when it gives it to the surrounding (moving piston). It's negative when it rceives it. By the force F due to the pressure P of the fluid, undergoing an expansion dx, the piston get displaced by the amount dx.
We can write: W = F.dx = P.S.dx = P.dV
dW = P.dV.
The total work done by the system (fluid) on its surrounding (piston) is positive: W = ∫ P.dV [from i → f]; i and f stand for the initial and the final states for the system and the surrounding.
With an isobaric process, that is with a constant pressure, we get: W = P ΔV ; or Wif = Pi. (Vf - Vi). The pressure P is mainained at its initial value Pi. For an isochoric process, that is at constant volume, W = 0.
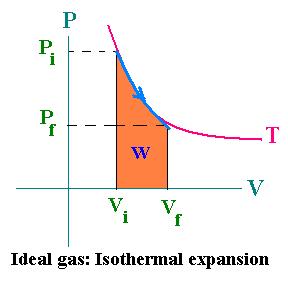In the case of an ideal gas, P = nRT/V; then dW = nRTdV/V. For an isothermal expansion, the integration gives:
Wif = nRT ln(Vf/Vi)
If Vf > Vi then W > 0
If Vf < Vi then W < 0
In the cas of an ideal gas in a quasi-static (in equilibrium) adiabatic process, we have
from the formula (6.2) : PVγ = Constant
Then P = PiViγ/Vγ. Therefore:
W = ∫ pdV = ∫ dV PiViγ/Vγ [Vi → V f]
= [1/(1 - γ)] PiVi [1/( Vfγ - 1 - 1) - 1/( Viγ - 1 - 1)]
= [1/(γ - 1)][PiVi][1 - (Vi/Vf)γ - 1]
W = [PiVi/(γ - 1)][1 - (Vi/Vf)γ - 1]
