1. Temperature scalar field
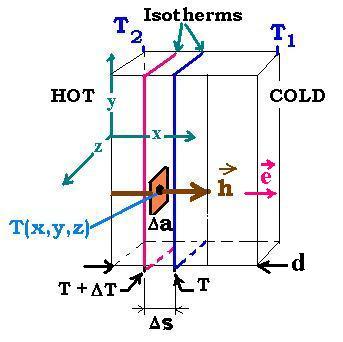
A field is a quatity that depends upon a position in space. A scalar field is
caracterized by a single number ( which could change in time) at each point. One example is the
temperature at a point as it's shown in the figure.
The block (cube) is heated and gives off heat outside it. The temperature of this
body varies from point to point. At the position (x,y,z), its value is T(x,y,z). The temperature
T2 is greater than T1, because heat flows from the hotter place to cooler.
The lignes (curves) or the surfaces where the temperature has the same value are called isotherms
or isothermal surfaces.
2. Heat vector field: the flow
A vector field is caracterized by its three components, its direction and its magnitude
as a normal vector. The vector h shown in the figure is the heat flow vector. It varies
from point to point. What makes this vector exist? The answer is difference in temperature. Let's recall
that the flow is the energy transferred by unit time, through a surface. The heat flow h is
the heat (thermal energy) per unit time ΔJ that passes through the surface element Δ a. Let's write:
h = Δ J/Δa
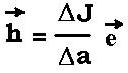
e is the unit vector in the direction of flow.
Remarks:
1. The vector h is perpendicular to the surface element Δa. If it is not the
case, it will simply be the projection of a vector h0 on the axis perpendicular to the
surface element and we can just write h = h0 cos (h,h0) or h = h0.n;
that is the scalar product of h0 and n; where n is the normal vector to the surface
element Δa.
2. The heat flow is directional. Heat flows in different directions across the body (cube). The isotherms
are not necessarily planes surfaces. The cube drawn in the figure represents a small part of a material.
3. The gradient of the temperature field
Now, let's evaluate the variation of the temperature. For two nearby points related to
T + ΔT and T, separated by &Delata;S over the x axis, we can write the following
differential:
ΔT = (∂T/∂x)Δx + (∂T/∂y)Δy + (∂T/∂z)Δz = ∇T . ΔR
Where ΔR = (Δx,Δy,Δz) and ∇ is the del or grad operator. When it acts on T, we have
∇T and we say gradiant of T or del T or grad T.
Remark:
∇ acts on a scalar. But it can alson act on a vector. For example: ∇. h . In this case, each
componebt of &nabla acts on each component of h; we have, here, the dot product of two vectors.
4. The flux of the vector heat flow
We know that the heat flow is the thermal heat per unit time. Now, we define the flux of a vector heat as the flow per unit surface. It is also the flow that passes across a surface. The flux of the vector heat h is written as:
Flux out of the surface element is: h Δa
The flux related to the surface of the cube (surface closed) is:
Flux out of the cube = ∫cube h Δa
.
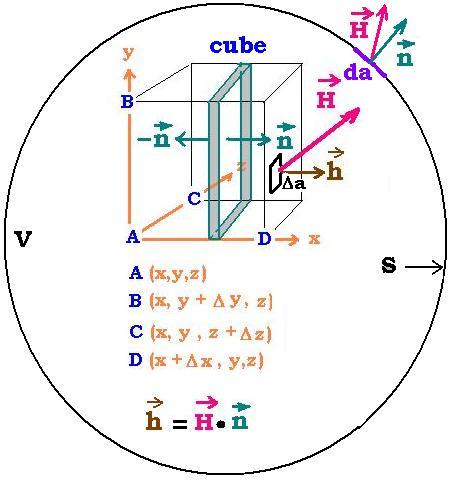 The flux of H across the left face is Flux-Left = - Hx Δy Δz
The flux of H across the left face is Flux-Left = - Hx Δy Δz
The flux of H across the right face Flux-Right is given by the relationship:
[Flux-Right - ( - Flux-Left)]/Δx = [∂Hx/∂x]Δy Δz
The flux across both the left and the right faces is:
Flux-Right + Flux-Left = [∂Hx/∂x]Δx Δy Δz
Or :
Flux-Right + Flux-Left = [∂Hx/∂x] ΔV
Where the unit volume Δ V = Δx Δy Δz
The same reasoning for the top and botton faces give:
Flux-Top + Flux-Botton = [∂Hy/∂y] ΔV
Flux-Front + Flux-Back = [∂Hz/∂z] ΔV
The total flux outward the cube is the some of all the fluxes accross the 6 faces:
Thus:
Total flux = [(∂/∂x, ∂/∂y, ∂/∂z). H ] ΔV = ∇ . H ΔV
∇ . H is the divergence of the vector heat H.
In other terms:
∫cube H . n da = ∇ . H ΔV
If we cut the cube into two parts, le fluxes of the two interior faces ( n and - n)
will cancel out; that is the integral over the two obtained cubes will give the same result as before. This result is valid for any number of cuts and any shape of surface. Then for a surface S that wrap the cube, whish is the volume element, we can integrate over all the volume elements ΔV to obtain the flux of the vector heat accross the surface S that wrap a volume V. Then:
∫S (H . n) da = ∫V (∇ . H) dV
Whish is the Gauss' theorm.