1.Introduction

To set some results about the behavior of molecules in a gas, we make assumptions such as :

1. The numner N of molecules is large; each molecule has mass m and its size is negligeable compared to the average distance between moleculles.
2. In its motion, a molecule obeies to the Newtonian mechanics
3. A molecule moves freely, except when it collides with another molecule or with the wall of the container. All collisions are elastic.
4. The molecules move randomly; taht is a molecule is equally likely to be moving in any direction.

2.Average velocity

For a molecule labeled i, its velocity v_i with the components (v_ix, v_iy, v_iz) in a coordinate system can take any direction. The average velocity over all N molecules in the box, along with the x axis is:

<v_x> = Σv_ix/N   (2.1)

A component of the velocity can have positive as well as negative values. These two values can occur with the same frequency (probability), therefore their contribution to the sum in the equation (2.1) is zero.
A same reasoning to the y and z components of velocity applies. Thus:

<v_x> = <v_y> = <v_z> = 0   (2.2)

This does not mean that a molecule in the gas does not move. It's true that the average molecular velocity is null, that is:

<v> = Σ v_i/N = <v_x> i + <v_y> j + <v_z> k = 0    (2.3)

(i, j and k are the vectors unit in the coordinate system). But, indeed, a molecule has an average molecular speed and the molecule labeled i moves at the speed v_i such as:
v_i² = v_ix² + v_iy² + v_iz². Since the directions x, y and z are equivalent, we can write:
<v_x²> = <v_y²> = <v_z²>, we have then the mean square speed :

<v²> = Σ v_i²/N = <v_x²> + <v_y²> + <v_z²> = 3. <v_x²>    (2.4).

That is very important result used in Thermodynamics.

3.Expression of the pressure

Let's consider a molecule i moving in the box hits the wall of area S = L_y. L_z. Its velocity changes from v_i = (v_ix, v_iy, v_iz) to v'_i = (v_ix, - v_iy. v_iz). The resultant momemntum of the molecule of mass m is Δp = 2m(v_ix - (- v_ix), v_iy - v_iy, v_iz - v_iz) = (2mv_ix, 0, 0). Its magnitude is:
Δp = 2mv_ix     (3.1)
Now, During this change in the momentum of the molecule, the wall received an impulse I_ix from the molecule i by collision. This impulse is expressed by
I_ix = F_ix. ΔT.     (3.2)
F_ix is the force related to the change in the momentum.
This impulse is equal to the change in the momentum.
During this time intervall ΔT ( considered sufficiently small to disregard the occurence of another molecule-molecule collision),the probability that the colliding molecule i has the velocity v_ix is the probability to be at the range l_x = v_ix(ΔT/2); that is l_x/L_x.
The average value of the impulse delivered to the wall by the molecule is the product of the collision probabilty and the impulse of the collision. We have:
<I_ix> = 2mv_ix. v_ix(ΔT/2)/L_x = m v_ix² ΔT/L_x
Summing over all the molecules, we find:
<I_x> = (m ΔT/L_x) N Σv_ix²/N = (m N ΔT/L_x)<v_x²> = (m N ΔT/3L_x) <v²>

<I_x> = m N ΔT <v²>/3L_x     (3.3)

From the equation (3.2), the average force component <F_x> is: <F_x> = <I_x>/ΔT
The pressure is then:
P = <F_x> /S = <F_x> /L_y. L_z = <I_x>/ΔT /L_y. L_z =(m N ΔT/3L_x) <v²>/ΔT /L_y. L_z = m N /3V <v²>. Where the volume V is equal to L_x.L_y.L_z. We find then:

PV = Nm<v²>/3     (3.4)

4.Internal energy and temperature

Let's consider a monoatomic gas whose molecules behave as a point particles so that the potential energy between them is neglected. Plus, there are no rotations nor vibrations related to the molecules; the internal energy U of the system consists of the translational kinetic energy of the molecules K_i; that is:
U = ΣK_i = (1/2)m Σv_i² = (N/2)m <v²> = N <K>;      (4.1)

<K> = Σv_i²/N = (1/2)m <v²>      (4.2)

is the mean value of the kinetic energy of the molecules.
We have U = ΣK_i = N ΣK_i/N = N <K>       (4.3)
Combining (2.4) and (3.1), we get for an ideal gas: U = (N/2)m <v²> = (N/2)m 3PV/Nm = (3/2)PV = (3/2) nRT = (3/2) (N/N_A)RT. Then:

U = (3/2)nRT = (3/2) NkT      (4.4)

Where N_A = 1.023 x 10 ²³ the Avogadro's number and k = R/N_A = 1.38 x 10 ^{- 23} T/K the Boltzmann Constant. From the equations (3.1) and (3.4), we get:

<K> = (3/2) kT      (4.5)

The root-mean-square of speed v_rms is defined as:
v_rms = [<v²>]^1/2; that is by equating (3.2) and (3.5) :

v_rms = [3kT/m]^1/2

At very low temperature (T → 0); that gives v_rms → 0 which means that the molecules become at rest! That's incorrect, because the result is based on the Newton's laws which do not adequately describe the motion of the molecules. Quantum Statistical Mechanics must be used for a correct description of the molecular motion in gases.

Equipartition energy theorem

The average translational kinetic energy is given by the equation (4.5), that is : <K> = (3/2) kT = 3. [(1/2)kT]
the factor three comes from the fact that there are three translational degrees of freedom for each monoatomic molecule.
For an ideal gas the mean molecular mechanical energy <E> is the mean molecular kinetic energy <K>, that is <E> = 3. [(1/2)kT]
The generalisation of this result is the equipartition of energy theorem

The average molecular mechanical energy <E> for a system of molecules at temperature T, with each molecule having ν degrees of freedom is <E> = ν [(1/2)kT]     (4.6)

<E> = ν [(1/2)kT]      (4.7)

For a linear diatomic molecule, we have three translational degrees of freedom related to the motion of the center of mass and two degrees of freedom corresponding to the rotation of the two atoms around the two related perpendicular axes. We have: ν = 5. Adding two degrees of freedon regarding the vibrational motion, we get, in the total ν = 7.

5. Molar heat capacities' relationship

For an ideal gas, at constant volume ( dV = 0).
According to the first law of Thermodynamis , we have : dQ = dU = nC_V dT      (5.1)
For a monoatomic gas, from the equation (4.4), we have: U = (3/2)nRT ; then dU = (3/2)nR
Differentiating PV = nRT, we have PdV + VdP = nRdT      (5.2)
Now, at contant pressure, dQ = nC_PdT , and PdV = nRdT; then:
The 1st law gives: dQ = dU + PdV = dU + nRdT      (5.3)
For this isobaric process: dQ = dU + nRdT = nC_PdT,      (5.4)
Since for an ideal gas, the internal energy depends only on the temperature, for the same change in temperature, the change in inernal energy is the same for a constant volume and for a constant pressure processes.
Substituting (5.1) in ( 5.4), we find: nC_PdT = nC_V dT + nRdT , then:
C_V + R = C_P.

R = C_P - C_V      (5.5)

For an ideal gas:
We know from the equation (3.4) that for an ideal gas U = (3/2) nRT,then
dU = (3/2) nRdT.
As dU = nC_VdT,then C_V = (3/2)R and C_P = (3/2)R + R = (5/2)R

For a diatomic and polyatomic gases, <E> = ν [(1/2)kT]. using N = nN_A, we have
U = N <E> = nN_Aν [(1/2)kT]. Since N_Ak = R, we find: U = n ν [(1/2)RT]; then
C_V = (1/n) dU/dT = (1/2) νR.
This result is in a good agreement with the predictions of the kinetic theory, but solely at low temperature.

For a solid with N atomes attached to each other with an ideal spring, no rotation can occur. The main degrees of freedom that we have here are the 3 translational and the three vibrational. The internal energy of the solid with N atoms is the sum of kinetic and potential erergies of vibration of the atoms. We have ν = 6, then

C_V = 3R

called the Dulong-Petit law.

6. Adiabatic process

An Adiabatic process stands for no change of energy between the systema and its surrounding; that is dQ = 0. This process occurs rapidly enough so that the heat added is negligible (compression of the fuel-air in the automobile engine).

For an ideal gas, according to the 1st law, an infinitesimal adiabatic process can be written as:
dQ = dU + pdV = nC_V dT + PdV = 0    (6.1)
Differentiating PV = nrT, we get:
PdV + VdP = nRdT
From the equation R = C_P - C_V and using the equation: γ = C_P/C_V, we get:
PdV + VdP = n(C_P - C_V)dT = ndTC_V(γ - 1) = ndTC_V γ - ndTC_V
From the equation (6.1), PdV + VdP = ndTC_V γ + PdV. We get then:
VdP = ndTC_V γ = - γPdV
dP/P = - γ dV/V
ln(P) = - γln(V) + Constant
ln(P) + γln(V) = Constant
ln(PV^γ) = Constant     (6.2)

For an ideal gas at an adiabatic process, we have :
PV^γ = Constant

7. Maxwell-Boltzman distribution

Let's consider a function f whose argument is the velocity v = (v_x, v_y, v_z) and that is the product of three functions as follows:
f(v) = f_x(v_x). f_y(v_y). f_z(v_z)       (7.1)
A partial derivative gives:
∂f(v)/∂v_x = [∂f_x(v_x)/∂v_x]. f_y(v_y). f_y(v_z)       (7.2)
∂f(v)/∂v_x = [∂f(v)/∂v]. [∂v/∂v_x]      (7.3)
∂v/∂v_x = ∂[v_x² + v_x² + v_x²]^1/2/∂v_x = (1/2) . 2 v_x/v = v_x/v       (7.4)
The equation (7.2) becomes:
[∂f(v)/∂v]. v_x/v = [∂f_x(v_x)/∂v_x]. f_y(v_y). f_y(v_z)       (7.2')
By deviding by f(v), we get:
[∂f(v)/∂v]. v_x/v f(v)= [∂f_x(v_x)/∂v_x]/f_x(v_x)       (7.2")
Therefore:
[∂f(v)/∂v]/v f(v)= [∂f_x(v_x)/∂v_x]/f_x(v_x)/ v_x             (7.5)
We have the same relationships about y and z components:
[∂f(v)/∂v]/v f(v)= [∂f_y(v_y)/∂v_y]/f_y(v_y)/ v_y           (7.5')
and
[∂f(v)/∂v]/v f(v)= [∂f_z(v_z)/∂v_z]/f_z(v_z)/ v_z           (7.5")
Rewrite (7.5):
[∂f(v)/∂v]/v f(v)= [∂f_x(v_x)/∂v_x]/f_x(v_x)/ v_x = Constant = a             (7.6)
∂f_x(v_x)/f_x(v_x)= a . v_x ∂v_x             (7.7)
Integrating, we obtain:
ln[f_x(v_x)] = (1/2) a v_x² + Constant
Thus: f_x(v_x) = exp [(1/2) a v_x² + Constant] = Constant exp [(a/2) v_x²]             (7.8)
Normalizing the function f_x(v_x), we would get:
∫ f_x(v_x)∂v_x = 1; which is never possible because ∫ exp [(a/2) v_x²]∂v_x diverge if a the constant "a" is positive. It follows that the constant "a" must be negative. We change it by rewriting the constant "a" , " - a" instead, with the constant "a" positive; Then:
f_x(v_x) = Constant exp [- (a/2) v_x²]            (7.9)

Normalizing, we have: 1 = Constant ∫ exp [- (a/2) v_x²] dv_x (- ∞ → ∞)
= Constant . 2. ∫ exp [- (a/2) v_x²] dv_x (0 → ∞)

Using the result: ∫ exp[- a x²]dx (0 → ∞) = I(0) = [π/4a]^1/2 from the probability integrale, It follows that:
1 = Constant.2.[π/4(a/2)]^1/2, Then

Constant = [a/2 π]^1/2             (7.10)

We have then:
f(v_x) = [a/2 π]^1/2 exp [- (a/2) v_x²]             (7.11)

Now, we will determine the constant a. Equating (3.2) and (3.5), we find:

<v²> = 3kT/m      (7.12)

Using the distribustion of speeds , we can write:
<v²> = ∫ f(v) dv v²
From the equation (1.4), we have <v²> = 3 <v_x²> = 3 ∫ f(v) dv v_x²
= 3 ∫ v_x² . f_x(v_x) f_y(v_y) f_z(v_z) dv_x dv_y dv_z
= 3 [a/2 π]^3/2 ∫ v_x² . exp [(a/2) v_x²] . (2π/a)
= 3 [a/2 π]^3/2 . [2 (π/4)(1/(a/2)^3/2] . (2π/a) = 3/a      (7.13)
Equating (7.12) and (7.13), we get:
a = m/kT
     (7.14)

Using (7.11), he equation (7.1) becomes:
f(v) = [a/2 π]^3/2 exp [- (a/2) v²]
since dv = v² dv sinθ dθ dφ, we get e function depending solely in the magnitude of the velocity, that is the speed:
f(v)dv = 4π [a/2 π]^3/2 exp [- (a/2) v²] v² dv
Let's write:

f(v) = 4π[m/2πkT]^3/2 v² exp [- (m/2kT) v²]     (7.15)

That is the Maxwell velocity distribution.

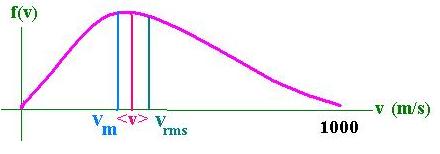We want now to calculate:<v>, the average molecular velocity
<v> = ∫ v f(v) dv = 4π[m/2πkT]^3/2 ∫ v³ exp [- (m/2kT) v²] (0 → + ∞)
Since I(3) = 1/2a², then:
<v> = (1/2) 4π[m/2πkT]^3/2 (2kT/m)² = [8kT/πm]^1/2

<v> = [8kT/πm]^1/2

Now, we want to calculate:v_m, the more likely velocity for a molecule :
It is found by differentiating f(v) and to set it equal zero in order to find the maximum. It follows that:
df(v)/dv = 4π[m/2πkT]^3/2 d[v² exp [- (m/2kT) v²]]/dv = 0
2v exp [- (m/2kT) v²] - 2(m/2kT) v³ exp [- (m/2kT) v²] = 0
2v - 2(m/2kT) v³ = 0, that is: v² = 2kT/m, therefore:

v_m = [2kT/m]^1/2

We can remark that : v_m < <v> < v_rms

---