A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
The Born's approximation
The Born's approximation is well known to give a quick solution
for the Diffusion equation (or PDE : Partial Differential Equation) in the scattering formalism.
1. The Born series
Let's rewriteFrom the general solution of the equation of diffusion:
ψk(r) = eik.r -1/4π∫eik|r-r'|/|r-r'| U(r')ψk(r') dr' (1)
We can see in the above equation that the term ψk(r') relating to the wave function is
iterative. Let's then rewrite the same equation by expressing
ψk(r') again in the second term of the second member in the equality. We have then:
ψk(r) = eik.r -1/4π∫eik|r-r'|/|r-r'| U(r') (eik.r'
-1/4π∫eik|r'-r"|/|r'-r"| U(r") ψk(r")) dr'dr"
= eik.r -1/4π∫eik|r-r'|/|r-r'| U(r') (eik.r') +
(-1/4π)2∫eik|r-r'|/|r-r'| U(r') ∫eik|r'-r"|/|r'-r"| U(r") ψk(r")) dr'dr" + ... (2)
This is known as Born series.
Commonly, we use only the two first term, and then keep
the expression (1).
2. The Born approximation
The main idea is make the expression of the ψk(r),
which is an asymptotic scattering, converge.
When r tends to ∞ we can write:
|r - r'| = ((r- r')2) 1/2 = ((r2 - 2 rr'+ r'2)1/2 = r ( 1 - 2 ur'/r + (r'/r)2)1/2 (3)
U is the unit vector of the vector r.
r>>r' ther (r'/r)2 is neclected, then:
|r - r'|= r( 1 - 2 ur'/r)1/2 = r ( 1 - 2 ur'/r)1/2 = r(1 - ur'/r) (4)
The Green's function :
Gk(r)= (-1/4π) eik|r - r'| /|r - r'|
ca be written as:
Gk(|r - r'|)= (-1/4π)eikr(1 - ur'/r) eikur /r(1 - ur'/r).
Neglecting again r' beside r, we have then:
Gk(|r - r'|)= (-1/4π)eikr e - ikur' /r (5)
The function (1) can be written as :
ψk(r) = eik.r -1/4π∫eikr(1 - ur'/r)/(r(1 - ur'/r)) U(r')ψk(r') dr' = eik.r -1/4πeikr∫e - ikur')/(r(1 - ur'/r)) U(r')ψk(r') dr'
ψk(r) = eik.r - (1/4πr) eikr ∫e - ikur' U(r')ψk(r') dr' (6)
Now, take the first order of the function ψk(r'), that is
ψk(r') = eikr'. It follows that:
ψk(r) = eik.r - (1/4πr) eikr ∫e - ikur' U(r')eikr' dr'
= eik.r - (1/4πr) eikr ∫e - ikur'+ikr' U(r') dr'
ψk(r') =
eik.r - (1/4πr) eikr ∫e ir'(k -ku) U(r') dr' (7)
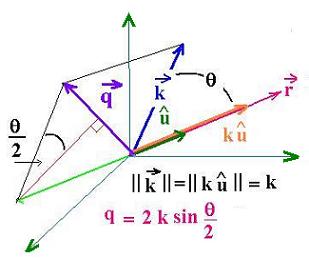
The quantity k - ku is called the momentum transfert. Let
q - k - ku ,as shown in the figure below:
3. The scattering amplitude
The relationship (7) becomes:
ψk(r') = eik.r - (1/4πr) eikr ∫e iqr' U(r') dr' (8)
Letting:
f(q) = - (1/4π) ∫e iqr' U(r') dr' (9)
Then:
ψk(r') = eik.r + eikr/r f(q) (10)
The related scattering cross section is:
σ((q) = |f(q) |2 = | - (1/4π) ∫e iqr' U(r') dr'|2
Or:
σ((q) =(1/16π2) | ∫e iqr' U(r') dr'|2 (11)
Let's suppose that the equation (1) is the Schr�dinger equation.
k2 = 2mE/(h/2π)2, U(r') = 2mV(r')/(h/2π)2
Where m is the mass of the particle, E is its kinetic energy, V is its potential energy, and h the Planck's constant
We consider that the potential is central. Then : V(r'→) = V(r)
The relationship (9) becomes:
f(q) = - m/2π(h/2π) ∫e iqr' V(r') dr' (12)
Let's consider the solid angle : r'2 dr'sinθdθ dφ around the vector q, then:
∫e iqr' V(r') dr'= 2π∫∫e iqr'cos(θ) V(r') r'2 dr'sinθdθ
For r': the integrale is from 0 to ∞
For θ from 0 to π
∫e iqr' V(r') dr' = 2π∫∫e iqr'cos(θ) V(r') r'2 dr'sinθdθ (13)
∫e iqr'cos(θ) sinθdθ = ∫e iqr'cos(θ)d(-cosθ)
= (- 1/iqr') (e- iqr' - eiqr') = (1/iqr') (2i) (sin(qr')) = (2/qr') sin(qr') (14)
Then:
f(q) = - m/2π(h/2π) ∫e iqr' V(r') dr'= - m/2π(h/2π) (2π) 2 ∫ V(r') 'sin(qr') /(qr') r'2 dr'
f(q)Born=
(-2m/(h/2π)2) ∫ V(r') 'sin(qr')/(qr') r'2 dr' (15)
|
|
|