Young's double-slit Interference

1. Interference fringes

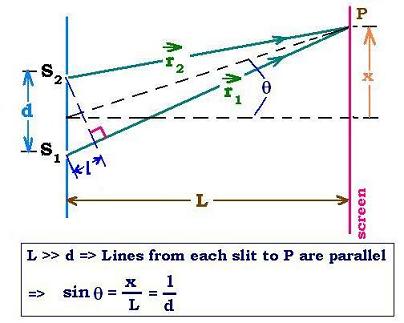
Simple-slit experiment explains diffraction phenomenun, whereas double-slit explains dinterference phenomenun.

Two light rays pass through two slits, separated by a distance d and reach a screen at a distance, L from the slits.
As L >> d, we can consider that the lignes from the two slits to the point P are parallel; so r₂ - r₁ = l = d sinθ = d x/L.

When the two rays pass through the two slits, the condition for constructive interference is that = nλ, where n is an integral number and λ is the wavelength of the ray (wave).




Constructive interference: d sinθ = nλ
Destructive interference: d sinθ = (n + 1/2)λ

On the screen, the bright bands correspond to the points of constructive interference, and the dark bands correspond to the points of destructive interference. Both constite waht we call interference fringes.

From x = L sinθ = L d sinθ/d , we have:
x_bright = n L λ/d for the bright bands, and
x_dark = (n + 1/2) L λ/d for the dark bands.

The bright bands are spaced by the distance:
Δx = x_next-bright - x_bright = [(n + 1) L λ - n L λ]/d = L λ/d

2. Intensity distribution

For each point "P" of the screen, the intensity I of light is calculated using the principle of superposition. It is expressed as:
I = S = (1/2) ε_o E₁₂², where E₁₂ is the vectorial sum of the two electric field E₁ and E₂ of the rays comming from the slit S₁ and S₂.

If E₁ = E_o sin(ωt), and
E₂ = E_o sin(ωt +φ), are the electric fiels of each slit, then
E₁₂ = E_o [sin(ωt) + sin(ωt +φ)].

sin(a + b) = sin a cos b + cos a sin b
sin (a - b) = sin a cos b - cos a sin b
By addition, we have sin (a + b) + sin (a - b) = 2 sin s cos b
with a + b = ωt + φ and a - b = ω t, that is a = ωt + φ/2 and b = φ/2
we obtain sin(ωt) + sin(ωt +φ) = 2 sin(ωt + φ/2) cos (φ/2)

E₁₂ = 2 E_o cos (φ/2) sin(ωt+ φ/2), that oscillates with the amplitude 2 E_o cos (φ/2),

E₁₂² = 4 E_o² cos² (φ/2) sin²(ωt + φ/2)

If I_o is the intensity of light for a single slit, that is I_o = constant x E_o², we have also
I₁₂ = constant x E_o² = I_o x 4 cos² (φ/2)
I₁₂ = 4 I_o cos² (φ/2)

With φ/2 π = d sin θ/λ, we have:

I₁₂ = 4 I_o cos² (πd sin θ/λ) = 4 I_o cos² [(πd/λL) x]

3. Diffraction grating

For a grating with N slits, the total distribution of the intensity on the screen corresponds to the sum of the individual electric field for each slit "i", that is:
I = (1/2) c ε_o E², with E = ∑ E_i
If E_i = E_o sin(ωt + iφ), then:
E = E_o ∑ sin(ωt + iφ), with i varies from 0 to N -1. Using the comples notation, (j² = - 1), we have:
E = E_o Img [∑ exp{j(ωt + iφ)}]
But ∑ exp{j(ωt + iφ)} = exp{j(ωt} ∑ exp{j iφ)}; and
∑ exp {j iφ} = 1 + exp {jφ} + exp {jφ}¹ + exp {jφ}² + ... + exp {jφ}^{N - 1}

We know that : 1 + x + x² + x³ + ... + x^{n - 1} = (xⁿ - 1)/(x - 1)

Thus:
∑ exp {j iφ} = ( exp {jφ}^N - 1)/(exp {jφ} - 1) = (exp {jNφ} - 1)/(exp {jφ} - 1)

We know that : exp{jx} + exp {- jx} = 2j sin x

Then:
∑ exp {j iφ} = (exp {jNφ/2} - exp {- jNφ/2)/(exp {jφ/2} - exp {- jφ/2}) x exp {jNφ/2}/exp {jφ/2} = (2j sin(Nπ/2))/(2j sin(φ/2)) x exp {j(N - 1)φ/2} = (sin(Nπ/2))/(sin(φ/2)) x exp {j(N - 1)φ/2}

Then:
∑ exp{j(ωt + iφ)} = exp{j(ωt} (sin(Nπ/2))/(sin(φ/2)) x exp {j(N - 1)φ/2}
And:
Img [∑ exp{j(ωt + iφ)}] = Img [(sin(Nπ/2))/(sin(φ/2)) exp j{ωt + (N - 1)φ/2}]

Finally:

E = E_o sin[ωt + (N-1)φ/2](sin(Nφ/2))/(sin(φ/2))
And: I = I_o sin²(Nφ/2))/(sin²(φ/2))
Known as Single slit Fraunhofer diffraction
Where: I_o = (1/2)cε_o E_o² sin²[ωt+(N-1)φ/2]

4. Particular cases

4.1. No slits
No slit: N = 0, we get: I = 0: no effects on the screen.

4.2. One slit
Single slit: N = 1, we get: I = I_o, with I_o = (1/2)cε_o E_o² sin²[ωt], One slit gives diffraction effect.
We have seen Single slit diffraction that I = I_c sin² β / β², with I_c = (1/2)cε_o E_c² sin²(ωt), the intensity of incident rays at the center od the slit, β = (π a/λ) sin θ
Hence:
(1/2)cε_o E_o² sin²[ωt] = (1/2)cε_o E_c² sin²(ωt) sin² β / β²
That is:
E_o² = E_c² sin² β/β²
Or:
I_o = I_c sin² β/β²
Then:
I = I_o = (1/2)cε_o E_c² sin² β/β² sin²[ωt]


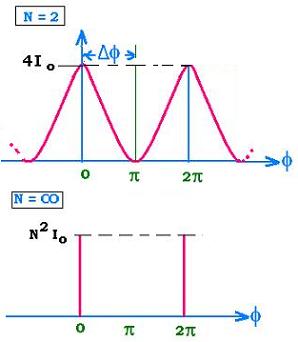
4.3. Double slit
Double slit: N = 2, we get: I = 4 I_o cos²(φ/2)
Where: I_o = (1/2)cε_o E_o² sin²[ωt+φ/2]
Comparing with the result above, we get the same result:
I₁₂ = 4 I_o cos² (φ/2). Thus: We have then:
I₁₂ = 4 I_c sin² β/β² cos² (φ/2)

4.4. Large number of slits
From the relationship: φ/2 π = d sin θ/λ, we differentiate to have:
Δφ/2 π = d cos θ Δθ/λ. With Δφ = 2π /N , we have:
1/N = d cos θ Δθ/λ. That is:
Δθ = λ/Nd cos θ
When N tends towards ∞ Δθ , and then Δ&phi tends towards zero.
When the number of slits is very large, N = ∞, Δφ becomes null. Δφ is equal to the difference between the first "zero" that occurs at φ = 2π/N and 0. In this case, we have a comb of equal intensities.