A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Green's function
Helmholtz's, Poisson's equations and the like are not obviously solved. Dealing with potentials, maily
in Electromagnetic field, solving such equations, requires an understanding and the use of the
Green's Function. The G'sF is a technique generally used to solve linear differential equations
in the presence of a source . In this lecture, we will use the Dirac Delta function, the Fourier Transform
to set the solutions of a PDE (Partial Differential Equation). We will set a general form for the solution
of the equation of diffusion, and consider the case of the Helmholtz's equation in three dimensions
with a second member not null.
1. Expression of the Green's function
The equation of diffusion has the form:
(Δ + k2) ψk(r) = U(r) ψk(r) (1)
Δ is the Laplacien, U(r) is the potential enegy and k is a parameter.
The operator Δ + k2 is called the kernel, and
S(r) = U(r) ψk(r) (3)
is called the source.
Now, let's write:
(Δ + k2) Gk(r) = δ(r) (4)
δ(r) is the Dirac's function.
It can be written as δ(3)(r) = δ(x)δ(y)δ(z)
The solution needed for the equation (1) is:
ψk(r) = ψ0,k(r) + ∫ Gk(r - r') S(r') dr' (5)
Where ψ0,k(r) is the solution for the homogenous equation, that is for S(r) = 0.
In this case the equation (1) becomes:
(Δ + k2) ψ0,k(r) = 0.
This stationary state is of the form:
ψ0,k(r) = eik.r (5')
To verify that ψk(r) is really the solution for the equation (1), apply
the operator Δ + k2 to it ( to the equation (5)) to find:
(Δ + k2)ψk(r)= (Δ + k2)ψ0,k(r) + ∫ (Δ + k2) Gk(r - r') S(r') dr' = 0 + ∫δ(r-r')S(r')dr'= S(r) .
dr' = d3(r')
2. Solutions of the Green's function for a PDE
Let's consider the example mentionned above and solve the equation (4).
First, write the Fourier Transform GFT(q) of the green function G(r).
GkFT(q) = (1/(2π)3)∫Gk(r)e-iq.r dr (6)
With:
Gk(r) = ∫ GkFT(q) e+iq.r dq (7)
For the delta function, according to ∫ f(x) δ(x-a) dx = f(a), we have:
δFT(q) = (1/(2π)3)∫δ(r)e- iq.r dr = (1/(2π)3)e- iq.0 = 1/(2π)3
Let's write:
δFT(q) = 1/(2π)3 (8)
Then:
δ(r) = (1/(2π)3)∫ e+iq.r dq (9)
Applying the kernel to the equality (7) yields:
(Δ + k2) Gk(r) = ∫(Δ + k2) GkFT(q) e+iq.r dq =
∫(- q 2 + k2) GkFT(q) e+iq.r dq (10)
According to (4), we can equate (9) and (10):
(- q 2 + k2) GkFT(q) = 1/(2π)3
Or:
GkFT(q) = - 1/(2π)3/(q 2 - k2) (11)
The relation (7) becomes:
Gk(r) =
(- 1/(2π)3) ∫ (e+iq.r /(q 2 - k2)) dq (12)
3. Integrated expresson of the Green's function for a PDE
We will use the following figure to integrate the relation above:
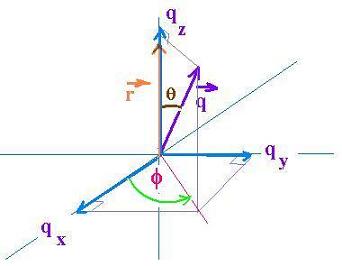
The spherical coordinates of the vector q are: q, θ, and φ.
Therefore, the integral element is q2dq sinθ dθ dφ.
φ from 0 to 2π, θ from 0 to π and q from 0 to ∞
We have chosen r parallel to kz, We have:
q.r = qr cosθ. Since
∫ dφ = 2π
Then, the relation (12) becomes:
Gk(r) = (- 1/(2π) 2) ∫ ∫ sinθ dθ (e+iq.rcosθ /(q 2 - k2)) q2 dq
(13)
= (- 1/(2π)2) ∫ (q2/(k2 - q 2)) dq ∫ d(- cosθ)(e+iq.rcosθ )
(cosθ from +1 to -1 and q from 0 to ∞)
= (- 1/(2π)2) ∫ (e+iq.r - e-iq.r) (q2/(q 2 - k2)) dq (1/iqr)
= (- 1/(2π)2/ir) ∫(e+iq.r - e-iq.r)(q/(q 2 - k2)) dq
= (- 1/(2π)2/ir)( ∫(e+iq.r (q/(q 2 - k2)) dq - ∫(e-iq.r (q/(q 2 - k2)) dq)
(14)
Let's change -q into +q in the second term. It becomes then
as the first, except the integrale varies from - ∞ to 0
for this second term. The sum becomes the first term integrated
from -∞ to +∞. We have then:
Gk(r) = (- 1/(2π)2/ir) ∫ (e+iq.r (q/(q 2 - k2)) dq)
(15)
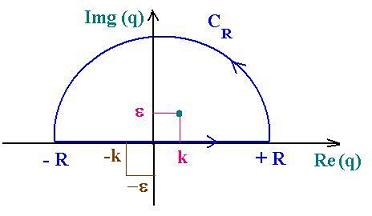
Now, we will integrate in the complex q plane. The following figure shows
two contours (-R,+R) and CR. Let's write:
∫contourGk(r) = ∫(- R,+ R) Gk(r) + ∫CR Gk(r) (16)
We have:
q 2 - k2 = (q - k) (q + k). Then two poles q = - k and q = + k.
In order to apply the residue theorem, we can write these two poles:
q- = limε = 0 - k - iε and
q+ = limε = 0 + k + iε
It follows that:
∫contour e+iq.r (q/(q + q-)(q + q+) dq =
∫ (- R, + R)(e+iq.r (q/(q - q+)(q + q+)) dq +
∫CR(e+iq.r (q/(q - q+)(q + q+)) dq (17)
According to the Jordan's lemma, the above second term
is null:
∫CR(e+iq.r (q/(q - q+)(q + q+)) dq = 0
Then:
∫contour e+iq.r (q/(q + q-)(q + q+) dq =
∫(- R,+ R)(e+iq.r (q/(q - q+)(q + q+)) dq (18)
The pole q- is outside the contour, then it will not contribute to the residue theorem.
Let's tend R towards ∞ and apply the residue theorem, then:
∫contour e+iq.r (q/(q 2 - k2) dq = 2iπΣ(Residues inside the closed contour) = Residue (q+)
Then:
∫contour e+iq.r (q/(q 2 - k2) dq = 2iπResidue (q+)
∫(-∞, + ∞)(e+iq.r (q/(q2 - k2)) dq = 2iπ Residue (q+)
= 2iπ (q - q+) e+iq.r q/(q - q+)(q + q+) (for q = q+)
= 2iπ e+i(q+).r (q+/(q+ + q+)
= 2iπ e+i(q+).r (q+)/(2q+)
= lim (ε = 0) 2iπ e+i(k + iε).r/2
= iπe+i(k).r
The relationship (15) becomes:
Gk(r) = (- 1/(2π)2/ir) iπ e+i(k + iε).r , or:
Gk(r) = - (1/4π) eikr /r (19)
The relation (5) becomes;
ψk(r) = ψ0,k(r) -1/4π∫ eik|r-r'|/|r-r'| U(r')ψk(r') dr' (20)
From the relationships (5') and (19), the general solution of the equation (1) is:
ψk(r) = eik.r -1/4π∫eik|r-r'|/|r-r'| U(r')ψk(r') dr' (21)
Remark:
The equation (19) is obtained with ε > 0. It's the outgoing solutioni, and written as:
Gk(+)(r)= (-1/4π) eikr /r (22)
In the opposite contour (negative region) ε < 0 is considered, so
the negative pole contributes. The other second solution is the incoming solution :
Gk(-)(r)= (-1/4π) e-ikr /r (23)
4. Particular case
The solution for the main equation (1), with S(r) = 0 is the relationship (5'), that is:
ψ0,k(r) = eik.r (24)
But this solution is not unique. In fact the complete solution for this homogenous
equation ((S(r) = 0) is:
ψ0,k(r) = C eik.r (25)
Where C is a constant.
In the case of k = 0, the main equation (1) becomes:
Δ ψ0(r) = U(r) ψ0(r),
or: Δ ψ(r) = U(r) ψ(r) (26)
The related particular solution is given by the relationship (21)
ψ0(r) = C - 1/4π∫ 1/|r-r'| U(r') ψ0(r') dr' (27)
The particular case used for the magnetic and electric potentials is to set
ψ (r) → 0 at infinity.
Therefore: C = 0. The equation:
Δ ψ(r) = S(r) (28)
has then the solution:
ψ0(r) = - 1/4π ∫ S(r') /|r-r'| d3(r') (29)
©: The scientificsentence.net. 2007.
|
|
|