A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Solids and Young's Modulus
Young's Modulus
1. Definitions
At a specified temperature, substances can exist in four different forms: solid, liquid,
gas, and plasma.
Exerting forces on substances, solid tends to keep its volume and its shape, liquid
tends to keep its volume not its shape, and gas and plamsa tend to keep
neither their shape nor their volume.
Generally, the separation between the two phases is not always clear, at 0o C,
water can be solid or liquid. A phase of substance is a matter of temperature. In the
normal conditions (pressure p = 1 atm, and temperature = room temperature
t = 20o C), we can know the phase of many substances such as steel, water, and air.
Solids are not easy to deform, that is changing their shape or size. Depending on
the force exerted on a solid, it can change slightly. Deformation on solids depends
also on their nature that is anisotropic or isotropic. We will focus here on isotropic
solids.
To deform a solid, force alone is
not sufficient to consider, the area where this force is applied is important as well. We define
the stress on the solid as the force exerted on the solid per unit area.
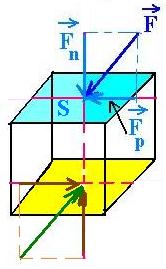
The force inward F is applied on a surface of area S, It can be the sum of two components:
normal force Fn and a parallel force Fp. In vector notation, we can
write F = Fn + Fp.
The stress σ is then:
σ = Fn/S + Fp/S = σn + σp.
σn is called the normal stress, and
σp is called the shear stress
To maintain the solid in the equilirium, The same force equal in magnitude and in
the opposite direction must be applied. This force is decomposed into its parallel and
normal components that will balance the same force components of the first force applied.
If the force is directed away from the solid, in this case the normal stress is called
tensile stress. If the same perpendicular force is applied inward on all the four surfaces of the solid,
the stress is called pressure
The dimention of stress is N/m2 that is Pascal Pa ( lb/in2 or psi:
pounds per square inch in British system. 1 lb/in2 = 6.9 kPa)
2. Young's modulus
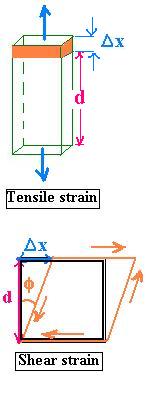The change in length is defined as:
εtc = Δx/d
called a tensile strain and a compressive strain
for a compression and elongation respectively.
The shear strain is defined as:
εs = φ = Δx/d
When the force applied on solid becomes important; that is in the fracture case, deformation
(then strain) can be proportional to the steress. This proportionality is called the
Young's mudulus. We can write then:
Y = σ/ε = (Fn/S)/(Δx/d)
Its dimension is a force per unit area; its SI unit is the pascal(Pa).
Similarly, the shear mudulus is defined as M = σs/εs = (Fp/S)/(Δx/d)
The bulk mudulus is defined as:
B = - V dP/dV = - ΔP/(ΔV/V)
That measures the required pressure P to compress a substance of volume V by the fraction ΔV/V.
Some examples:
| Substance | Y | M | B |
| Steel | 200 | 160 | 84 |
| Glass | 14 | 3 | 8 |
| water | 0 | 0 | 2.2 |
| Most gases | 0 | 0 | 1 x 10- 4 |
|
|
|
