Polarization of light

1. Introduction

We classify waves according to their direction of propagation. A transverse wave oscillates within a plane perpendicular to its direction of propagation; this is the case of waves on ropes or strings or the electric field of an electromagnetic wave. The oscillations of the longitudinal wave are parallel to its direction of propagation, this is the case of the sound waves. Water waves have both transverse and longitudinal components. Waves on ropes or strings, water waves, and sound waves are Mechanical waves. They require a medium in which they can travel and transport energy, and they can be described by Newton's laws. Electromagnetic waves travel within a medium or through vacuum. Traveling waves, as light, travel along a direction of propagation, in contrast with Standing waves, as in a guitar, that are confined to a certain space by boundaries. Waves can travel in two dimensions space, such as water waves that travel radially forming expanding concentric circles of crests (and troughs), separated by one wavelength, that are called wavefronts. Sound waves or light waves travel in three dimensions space forming concentric spherical surfaces as wavefronts within a uniform medium. These kind of waves, coming from a point source and traveling through all the space (three dimensions) are called spherical waves. At a large distance from the point source, the spherical wavefronts are generally planar wavefronts. Such waves are called plane waves. The solutions of the Maxwell's equations are plane waves. For these waves, if the direction of propagation is along "z", and the electric field E of the wave oscillates along "y", then the magnetic field B will oscillate along "x" (E is c times greater that B), the electric field E oscillates in th the plan "yz". We say that the transverse electromagnetic radiation oscillating in the plan "yz" is polarized. The plan "yz" the plane of polarization. In the present chapter, we will set the equation of the polarization for two waves in two dimensions and get the particular cases of linearly, circularly, and elliptically polarized waves. We will also show how a light polarizer and analyzer work and set Malus's law. Finally, we will describe some polarization effects such as dichroism, polarization by reflection and refraction including Brewster's law, and scattering.

2. Equation of polarization of two waves

Let's consider two waves with same amplitude and same frequency, but with different phases.
x = a cos (ωt - kz + α)    (1)
y = a cos (ωt - kz + β)    (2)

x/a = cos (ωt - kz) cos α - sin(ωt - kz) sin α     (3)
y/a = cos (ωt - kz) cos β - sin(ωt - kz) sin β     (4)

Multiplying (3) by sin β and (4) by sin α gives:
x/a sin β = cos (ωt - kz) cos α sin β - sin(ωt - kz) sin α sin β    ( 5)
y/a sin α = cos (ωt - kz) cos β sin α - sin(ωt - kz) sin β sin α     (6)

subtracting (5) and (6) gives:
(5) - (6) = x/a sin β - y/a sin α = cos (ωt - kz) cos α sin β - cos (ωt - kz) cos β sin α =
cos (ωt - kz) [cos α sin β - cos β sin α] = cos (ωt - kz) sin( β - α)     (7)

Multiplying (3) by cos β and (4) by cos α gives:
x/a cos β = cos (ωt - kz) cos α cos β - sin(ωt - kz) sin α cos β     (8)
y/a cos α = cos (ωt - kz) cos β cos α - sin(ωt - kz) sin β cos α     (9)

subtracting (8) and (9) gives:
(7) - (8) = x/a cos β - y/a cos α = sin (ωt - kz) cos α sin β - sin (ωt - kz) cos β sin α =
sin (ωt - kz) [cos α sin β - cos β sin α] = sin (ωt - kz) sin ( β - α)     (10)

The relationships (7) and (10) become:
x/a sin β - y/a sin α = cos (ωt - kz) sin (β - α)     (7')
x/a cos β - y/a cos α = sin (ωt - kz) sin (β - α)     (10')

Squaring and adding (7') and (10') gives:
(x/a)² + (y/a)² - (2xy/a²)[sin β sin α + cos β cos α] = sin²(β - α)
Or:
(x/a)² + (y/a)² - (2xy/a²) cos(α - β )= sin²(β - α)

Finally:

x² + y² - 2xy cos(α - β) = a² sin²(α - β)

3. Different cases

As light is a transverse wave, it can be then polarized in different waves. The polarization of light is always considered as along the electric field E rather than the magnetic field B (|E| = c |B|: E is c times greater that B). The plane that contains the field E and the direction of polarization is the plane of polarization: Here "yz". In this paragraph, the waves "x" and "y" can represent electric fields of an electromagnetic wave.

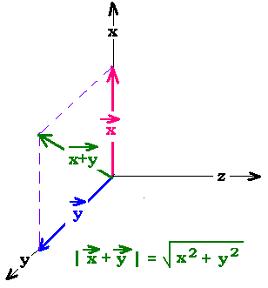
3.1. α = β

x² + y² - 2xy = 0
From which we have : (x - y)² = 0. Or x = y.
That is the resultant of the two waves in phase x and y is linearly polarized and oscillates along the line y = x.

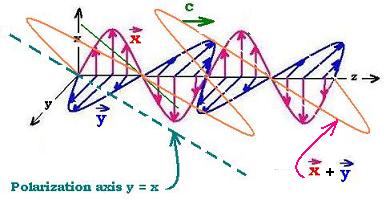
3.2. α = β + π/2

In this case, we have:
x² + y² = a²

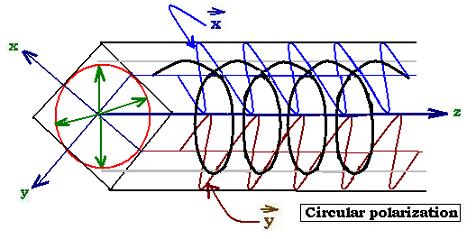
That is the resultant of the two waves in quadrature phase x and y is circularly polarized and oscillates in the plane "xy" along the "z" axis with fixed magnitude. The tip of the vector resultant rotates with constant frequency by tracing out a circle of radius "a" and moves forward along the "+z" axis (right), which is the direction of the propagation. If "x" rotates in the clockwise sense, the light is right-circularly polarized; in the counterclockwise sense, the light is left-circularly polarized.
If the amplitudes of the waves "x" and "y" are different, the resultant will be elliptically polarized.

4. How light is polarized

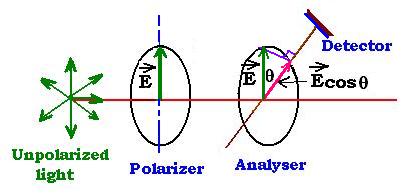
Unpolarized light is emitted in all the directions through space. It can be polarized by passing it through a polarizer. The well known device to polarize light is the Polaroid film that we use in sunglasses. The polarizer has a transmission axis by which lets passing light that has its plane of polarization parallel to it. The perpendicular ones will not be transmitted, and they are blocked by absorption or reflexion. We add a second polarized called analyzer that transmits only the component of E parallel to its transmission axis; that is the projection of the vector field E on the analyzer's transmission axis or E cosθ where θ is the angle between the polarizer's axis and the analyzer's axis. Since the intensity of light is equal to I = (1/2) c ε_o E², we derive then the relationship:
I = I_o cos² θ
That is the Malus's law.

5. Processes to polarize light

5.1. Absorption

A sheet of Polaroid uses the selective absorption called dichroism. The transmission axis of a dichroic material is due to a certain alignment of molecules or crystalline. Tourmaline crystal has the feature of dichroic material. Polaroid is made of stretched plastic colored with an ink that contains Iodine.

5.2. Scattering

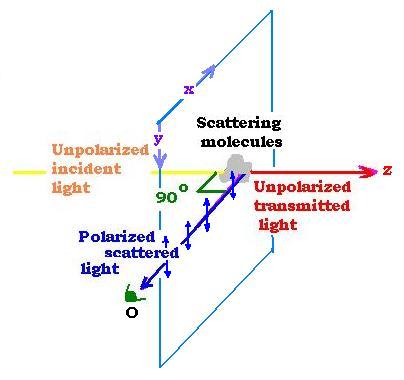
Skylight, that is light scattered from molecules of the atmosphere is polarized while they receive unpolarized light from the sun. Of course without those molecules the sky will be seen as it is at night. The Rayleigh formula show that the amount of scattering depends mainly on the wavelength of the scattered radiation, the shorter wavelengths are more scattered than the longer, and this is why the sky appears blue. The longer the light travels the atmosphere, the more the blue radiation depletes, this is why the sky is red at sunsets. During the day, we can remark, by observing scattered light coming from the direction perpendicular to the sun's direction is bright. The electric field of light that propagates along the z axis has no component along this axis because light is a transverse wave. Its electric field oscillates then in the polarisation plane "xy". The electric field viewed by the observer from the point "O", remains in the plane "xy" with no component in the "z" direction. Therefore, light from the scattering molecules (mostly blue) comes in at right angle to the incident beam of the unpolarized sunlight direction. The unpolarized transmitted light is mostly red.

5.3. Reflexion and refraction

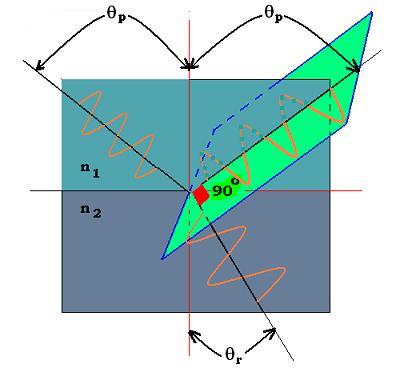
If an unpolarized light beam is incident on a glass surface, the reflected and refracted beam are partially polarized. At a particular angle, called polarizing angle θ_p, the reflected beam is totally polarized perpendicularly to the plane of incidence and then parallel to the reflecting surface. The refracted beam is parallel to the plane of incidence which contains the incidence beam, the normal to the surface and the reflected beam.
David Brewster (1781- 1868) discovered experimentally that the reflected and refracted beams, at complete polarization, are at right angle. From the law of Reflection, we have θ_incident = θ_reflected = θ_polarization = θ_p. According to Snell's law, we have: n₁ sin θ_p = n₂sin θ_r: where θ_r = θ_refracted. Therefore: θ_p + θ_r = π/2. Thus: sin θ_r = sin (π/2 - θ_p) = cos θ_p. Hence: n₁ sin θ_p = n₂ cos θ_p. Then: n₂ /n₁ = tg θ_p.Or:
n₂₁ = n₂ /n₁ = tg θ_p
That is Brewster's law.

Example:
For Air-Glass medium θ_p = arctg(n_Glass/n_Air) = arctg(1.5/1.0) = 56^o ≈ 1 rad.

Polarizers use also the feature of birefringence (or double refraction) of some materials such as Calcite (C_aCO₃) or crystalline quartz (SiO₂). The one of these two refracted rays is called the ordinary ray, the second the extraordinary ray. They are both polarized in two perpendicular planes of polarization. Notice that for those medium, Snell's law holds for the ordinary ray only; and holds for both of the rays if the optic axis of the medium is perpendicular to the plane of incidence.