A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Sound wave
1. Definitions
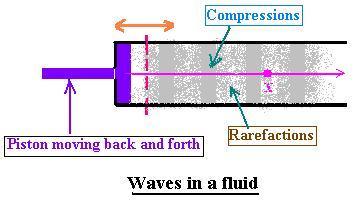
A sound wave is a mechanical wave with a frequency between
20 Hz and 20 kHz. Sound can travel in gases (air) or
liquids or even solids.
In this figure, the piston moves back and forth in a simple harmonic motion. The first
layer of fluid is compressed which transmits the force to its next neighboring
element. The force received from the piston forms a compression that travels
down through the fluid in the tube. Say the wave (perturbation) travels. During
the transmission of the wave, it formes the compressions regions with
higher density and pressure and the rarefactions regions with low density
and pressure formed during the return motion of the piston.
The element piston in the system can be replaced by a voice and the fluid
can be air, we have then a sound wave.
Note that this wave is a longitudinal wave with its wave-length λ that is the
distance between a compression and a rarefaction.
Now, suppose that a point (particle) in the fluid is located at a distance x. When a
compression reaches this point, it will moves in the direction of the propagation. Once
this point transmits its force to the point next to it, it will return (since it moves
back and forth and the motion is harmonic). This longitudinal motion for this point
can written as an harmonic wave function:
ψ(x,t) = A sin (kx - ωt) (1.1)
ψ(x,t) represents the longitdunal displacement of an element of the fluid; Where:
A is the maximum amplitude,
k = 2π/λ is the wave number,
ω is the angular frequency.
We have also:
v = ω/k, the speed of the wave.
2. The wave equation for sound
For each compression at the position x at the time t, corresponds a change in the
pressure ΔP(x,t) and a displacement Δx = ψ(x,t).
If Pe is the equilibrium pressure when no wave exists, then the
change in pressure can be written as: ΔP(x,t) = P(x,t) - Pe; where P(x,t)
represents the pressure of the fluid at time t at position x.
Since the pressure change is proportional to the related displacement, we can then write:
ΔP(x,t) = ΔPmax sin (kx - ωt) (2.1)
Now, let's take an element of the fluid of area S between x and x + dx when it is in
equilibrium . Its volume is Sdx. Because of a longitudinal wave, the two related
displacements are ψ(x,t) and ψ(x + dx, t). Thus the change in the volume
is ΔV = S [ψ(x + dx, t) - ψ(x , t)]. The fractional change of this
volume is: ΔV/V = [ψ(x + dx, t) - ψ(x , t)]/dx = dψ(x,t)/dx
ΔV/V = dψ(x,t)/dx (2.2)
Given the adiabatic bulk modulus, that expresses
a small change in pressure ΔP to a relative change in volume ΔV for an element of fluid is
written as:
Bs = - V (ΔP/ΔV) (2.3)
Thus, the equation (2.2) becomes:
dψ(x,t)/dx = - ΔP/Bs (2.4)
The x components of the two opposite forces exerted in the two opposite
faces of the volume elemet are: SΔP(x,t) and SΔP(x + dx, t). The net force
on the element is then:
dF = SΔP(x, t) - SΔP(x + dx, t) = S Bs [dψ(x,t)/dx|(x + dx) - dψ(x,t)/dx|x] = S Bs d[dψ(x,t)/dx]. (2.5)
Then:
dF/dx = S Bs [dψ(x,t)/dx]/dx = S Bs [d2ψ(x,t)/dx2] (2.6)
The acceleration of this element is: ax = d2ψ(x,t)/dt2. (2.7)
Its mass is dm = ρSdx; where ρ is the dnsity of the fluid.
Newton's second law can be written as:
ρSdx d2ψ(x,t)/dt2 = dF
Using the equation (2.6), it follows that:
ρ d2ψ(x,t)/dt2 = Bs [d2ψ(x,t)/dx2]. Then:
[d2ψ(x,t)/dx2] - (ρ/Bs) d2ψ(x,t)/dt2 = 0 (2.8)
3. Speed of sound in a fluid
We have seen that the equation of propagation of an
harmonic wave is :
[d2ψ(x,t)/dx2] - (1/v2) d2ψ(x,t)/dt2 = 0
(2.9)
Equating the equations (2.8) and (2.9), we obtain the expression of the speed of sound in a fluid:
v = [Bs/ρ]1/2 (3.1)
For an adiabatic process with an ideal gas,
we have PVγ = Constant
Differentiaring with respect to the volume, we get:
d[PVγ]/dV = 0
VγdP/dV + P γVγ - = 0
That is:
dP/dV + γ (P/V) = 0, or
dP/dV = - γ (P/V)
Using the definition of the bulk modulus, we obtain:
- γ (P/V) = - Bs/V
Thus:
Bs = γ P
from the relationship (.), the speed of sound in a fluid of density ρ becomes:
v = [γ P/ρ]1/2
(3.2)
If M is the molar mass of the fluid, then its mass m = n M = ρV. n is the number of moles
and V its volume. We have:
PV = nRT and
P /ρ = nRT/Vρ = (ρV/M)(RT/Vρ) = RT/M
The expression of the speed becomes:
v = [γ RT/M]1/2
(3.3)
4. Intensity of sound wave in a fluid
The expression of the related power is:
Power = Fx dψ/dt = ΔP S dψ/dt
The intensity is equal to: P/S = ΔP dψ/dt
From the equation (2.2) and using ΔP = - (ΔV/V)Bs from the definition
of the bulk modulus, and
dψ/dx = Ak cos(kx - ωt)
dψ/dt = - Aωcos(kx - ωt)
The expression of the intensity becomes:
We obtain:
I = - (ΔV/V)Bs (dψ/dt) = - ( dψ/dx)Bs (dψ/dt)
= - ( Ak cos(kx - ωt))Bs (- Aωcos(kx - ωt))= Bs A 2 k ω cos2(kx - ωt)
We know that the mean of cos2(kx - ωt) = 1/2; Then:
I = (1/2)Bs A 2 k ω
(4.1)
Using:
ΔP = - (ΔV/V)Bs = ΔP = - (dψ/dx)Bs = - Ak cos(kx - ωt)Bs
We find:
ΔPmax = - Ak Bs. I becomes:
I = (1/2)Bs A 2 k ω = [ΔPmax]2 ω / 2 k Bs
I = [ΔPmax]2/2 vρ
(4.2)
©: The scientificsentence.net. 2007.
|
|
|