A sigle wave
Superposition of waves
© The scientific sentence. 2010
| Standing waves
1. Interference of waves
1.1 The principle of superposition
Two or more waves can interfere, that is they encounter each other
or they are superposed. At any time and position, the resultant
y(x,t) is the sum of the wave function of each wave acting alone.
If fi are the individual wave functions, Σ fi is the resultant.
The principle of superposition states that the resultant wave
function is the sum of the individual wave functions.
Mathematically: y(x,t) = Σfi(x - vt)
Waves can be also reflected from boundaries or transmitted from a
medium to another.
Note that the wave function is linear and if yi(x,t) are solutions
of the wave equation; then Σyi(x,t) is also the solution of the wave
function. That is:
The solutions of the wave equation obey the principle of sperposition.
1.2 Constructive and destructive interference
We consider two harmonic waves to understand these phenomena.
The expressions of these two harmonic waves are:
y1(x,t) = A sin(kx - ωt + φ1)
y2(x,t) = A sin(kx - ωt + φ2)
Which are waves traveling in the same direction with the same
amplitude A, same wave number k and same angular frequency ω
but with different phase constants φ1 and φ2.
We use the principle of superposition to find the resultant wave due to
the interference of the two waves: y(x,t) = y1(x,t) + y2(x,t).
Then:
y(x,t) = A[sin(kx - ωt + φ1) + sin(kx - ωt + φ1)]
Using the trigonometric identity: sin (a + b) + sin (a - b) = 2 sin a cos b;
With: a + b = x and a - b = y , we get: a = (x + y )/2 and b = (x - y)/2 and furthermore:
sin (x) + sin (y) = 2 sin [(x + y )/2] cos [(x - y )/2]
It follows that:
y(x,t) = 2A sin [kx - ωt + (φ1 + φ2 )/2] cos [(φ2 - φ1)/2]
Let:
φ2 - φ1 = Δφ,
thus:
y(x,t) = 2A cos [(Δφ)/2] sin [kx - ωt + (φ1 + φ2 )/2]
The resultant wave is a harmonic wave with the same k (or λ),
the same ω (or T) and the same propagation direction.
The phase difference Δφ plays an important role in the intereference
phenomenun.
The waves are in phase, when Δφ = 0 (φ1 = φ2 = φ):
In this case:
y(x,t) = 2A sin [kx - ωt + φ] which is the constructive intereference
The waves are out of phase, when Δφ ≠ 0 (φ1 ≠ φ2):
The particular case is: Δφ = π rad (90o): the waves are
completely out of phase.
In this case:
y(x,t) = 0; which is the destructive intereference (crest on throug and
through on crest).
2. Standing waves
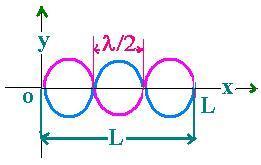
Let's consider an incident harmonic wave as a train wave (
wave that is lasts enough to consider its width L >> its wavelength λ
and its time t >> its period T. (see figure 5)
The created incident wave yi(x,t) propagating from the first boundary O to
the second boundary L in the + x direction is reflected on L. The reflected wave yr(x,t)
propagating in the - x direction intereferes with the incident wave. The resultant y(x,t) is
the interference wave that it will reflect back and forth from the boundaries establishing
stationary wave or standing waves.
Let:
The incident wave : y1(x,t) = A sin(kx - ωt) toward + x direction and
The reflected wave: y2(x,t) = A sin(kx + ωt) toward - x direction
These two waves have the same amplitude, the same k and same &omaga; that propagating in the
opposite directions with the same velocoty v = &omaga;/k.
Using the principle of superposition, we find the interference of these two harminic wave
is the following harmonic wave:
y(x,t) = A [sin(kx - ωt) + sin(kx + ωt)]
Since sin a + sin b = 2 sin[(a + b)/2]cos(a - b)/2], then:
y(x,t) = 2A cos ωt sin kx
The term : 2A cos ωt is the amplitude of the combined harmonic wave.
At any fixed position, the motion of an elemnt of the medium is a simple harmonic
motion oscilating as cos ωt.
Where do we have nodes and antinodes ?
The antinodal positions (extrema) are in the following places:
sin kx = 1 or - 1 → kx = π/2, 3π/2, 5π/2, ...; That is:
kxn = (n + 1/2)π or:
xn = (n + 1/2)λ/2 n = 0, 1, 2, 3, ...
The nodal positions (zero) are in the following places:
sin kx = 0 → kx = 0, π, 2π, 3π, ...; that is:
kxn = n π or:
xn = n λ/2 n = 0, 1, 2, 3, ...
Remark that the elements at these positions do not move.
Next, the boundary conditions give:
y(o,t) = y(L,t) = 0, that is sin kL = 0, and L = n λ/2 n = 0, 1, 2, 3, ...
Or:
L = n λn, /2 n = 1, 2, 3, ...
That is the length of the medium must be equal to an integer mutiple of
the one-half wavelength of the standing waves. In other words,
The allowed wavelengths for standing waves are:
λn = 2L/n (n = 1, 2, 3, ...)
Since v = λ ν, the restricted frequencies have the following values:
νn = n (v/2L) = n (F/μ)1/2/2L
The set of νn is called the natural frequencies or the harmonics.
The lowest ν1 = v/2L is the first harmonic, called the fondamental frequency.
ν2 the second harmonic, ν3 the third harmonic and so on.
3. Transmission & reflexion coefficients
Let's consider an incident harmonic wave yi propagating at + x direction
which, at the point origin, it
- reflects and produces the wave yr propagating at the inverse - x direction,
at the same wave number ki, and
- transmits the wave yt propagating the same + x direction
yi(x,t) = Aisin(kix - ωt)
yr(x,t) = Arsin(kix + ωt)
yt(x,t) = Atsin(ktx - ωt)
The continuity of the wave function at the point origin is:
y(0,t) = yi(0,t) + yr(0,t) = yt(0,t)
Aisin(- ωt) + Arsin(+ ωt) = Atsin(- ωt). That is:
Ar = Ai - At (3.1)
The continuity of the derivative of the wave function at the point origin is:
kiAicos(- ωt) + kiArcos( + ωt)
= ktAtcos(- ωt). That is:
ktAt = ki(Ai + Ar)
(3.2)
Using the relationship (3.1), we find:
The transmission coeffient:
Ct = At/Ai = 2 ki/(ki+kt)
and the reflexion coeffient:
Cr = Ar/Ai = (kt - ki) /(ki+kt)
Remark that if ki = kt, then:
Ct = 1, and Cr = 0 (Complete transmission: no reflected wave)
©: The scientificsentence.net. 2007.
|
|
|