A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Uncertainty principle
1. Gaussian wave packet
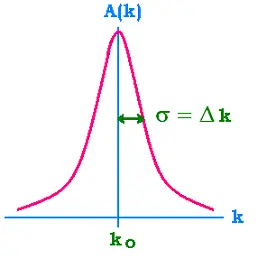
The Gaussian distribution (normal distribution) is written as:
P(x) = 1/σ(2π)1/2 exp {- (x - μ)2/2σ2} (1)
Which is already normalized.
σ2 is the dispersion or the variance that
shows how large data are spread around the location.
Its square root, σ, is called standard deviation. It shows how
large each value is distant from the neighbor other value.
The mean value of a variable "x" μ = <x> is called also the
average. It is the expectation value E(X) for a random variable
X associated to an event E and related to the theoritical probility
distribution.
In our case, the gaussian distribution (amplitude) is:
A(k) = 1/σ(2π)1/2 exp {- (k - ko)2/2σ2}
The average vulue for all wave numbers is ko. The good approximation is
to take the uncertainty of the variable "k" Δk equal to the
dispersion σ2. We know that the dispersion of "k" is defined as:
σk2 = E[(k - μ)2] = <(k - <k>)2>
= <k2> - [<k>]2
The wave function of the Gaussian packet is then:
ψ(x,t) = ∫ A(k) exp{i(kx - ωt)} dk =
= 1/σk(2π)1/2 ∫ exp {- (k - ko)2/2σk2} exp{i(kx - ωt)} dk
At t = 0, we have:
ψ(x,0) = ψ(x) = N ∫ A(k) exp{i kx} dk =
= 1/σk(2π)1/2 ∫ exp {- (k - ko)2/2σk2} exp{ikx} dk
Where N is set to normolize the function ψ(x).
Now: the integrale:
I = ∫ exp {- (k - ko)2/2σk2} exp{ikx} dk
Let k - ko = κ the dk = dκ
I = exp {ikox} ∫ exp {- κ 2/2σk2} exp{iκx} dκ
= exp {ikox J, where :
J = ∫ exp {- κ 2/2σk2} exp{iκx} =
∫ exp {[- (κ 2 - 2iκσk2x)]/2σk2} dκ
With :
κ 2 - 2iκσk2x = [κ - ixσk2]2 +
x2σk4
We have:
J = exp{- x2 σk2 /2} ∫ exp {[- (κ - ixσk2)2]/2σ2} dκ
let: z = [κ - ixσk2]/(2)1/2σk , then dz = dκ/(2)1/2σk and thus:
J = ((2)1/2σk) exp{- x2 σk2 /2}
∫ exp {[- z2]} dz
∫ exp {[- z2]} dz = (π)1/2
Refer to Result of
this integrale.
Hence:
I = exp {ikox (2)1/2σk exp{- x2 σk2/2}
(π)1/2
ψ(x) = N 1/σk(2π)1/2 exp {ikox
(2)1/2σk exp{- x2 σk2/2}
(π)1/2
ψ(x) = N exp{- x2 σk2/2} exp {ikox}
ψ(x) = N exp{- x2 σk2/2} exp {ikox} (2)
To find the value of N , we normalize the function as follows:
∫ ψ(x) ψ*(x) = 1. That is:
∫ N2 exp{- x2 σk2} dx =
= N2 ∫ exp{- x2 σk2} dx = 1
Let z = x σk, then dx = σk dz. we have then:
1 = N2 σk ∫ exp{- z2} dz
∫ exp{- z2} dz = (π)1/2 →
N2 σk (π)1/2 = 1 →
N= 1/σk1/2 (π)1/4
N = 1/σk1/2 (π)1/4 (3)
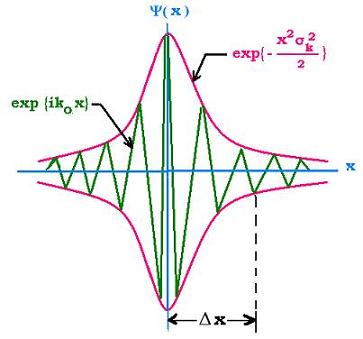
2. Uncertainty principle
We obtain an envelope exp{- x2 σk2/2} and
an oscillating factor : exp {ikox} for the wave function ψ(x). The
envolope has to be a Gaussian distribution and written as:
ψ(x) = 1/σx(2π)1/2 exp {- (x - μ)2/2σx2}.
The initial mean μ= <x> is choosen around x = 0 and leads to = 0. Then:
σx2 = <x2> - 02 = <x2>
That is:
exp{- x2 σk2/2} =
exp {- x 2/2σx2}
σk2 = 1/σx2.
That is:
σk = 1/σx
With:
Δk = σk 2 and Δx = σx 2.
We obtain the uncertainty principle of Heisenberg:
Δx Δk = 1 or according to De Broglie relationship: p = hk/2π, we find:
Δx Δp = h/2π
Δx Δp = h/2π (4)
The expression of σx is given at t = 0. In the ehe dispersive medium, this
expression changes and increases with time and the wave packet spreads out.
©: The scientificsentence.net. 2007.
|
|
|