Wave function

Suppose that we have a rope tied on an end and we wiggle once the other end; we get the sample of the wave called a pulse that moves along the rope.
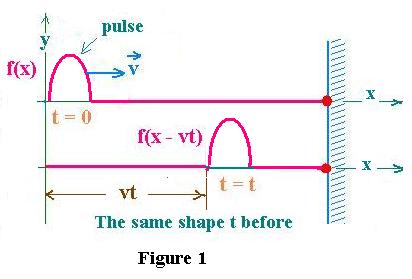
Let's reprensent the pulse in a (x,y) coordinate at the beginning ( t = 0) and at another time after ( t = t). The real situation is there are some dumping factors that make the pulse stop. We call this effect dispersion. In this case, the height of the pulse "y" decreases and its width "x" increases. In this article, we will disregard this effect and consider the pulse moves at constant velocity and its shape remains the same. Thereafter, if f is a function that represents the wave (anything that it propagates), we can write: y(x,t) = f(x - vt) for a pulse moving at + x direction; where v is the speed of the moving pulse. Similarly, if the pulse travels at - x direction, we can write: y(x,t) = f(x + vt). Recall, for the pulse:

y(x,t) = f(x - vt)

The function y(x,t) is called the wave function.
In the case of a wave on a rope, the wave function is the coordinate y(x,t) of an element of the rope at the the position x and at time t. It gives then the displacement over the axis y, of an element of the rope from its initial position (equilibrium position at y = 0 : undisturbed rope, streched horizontally).
Remark that the main features of the propagating pulse are: qualitatively: Its speed, the time and its displacement. quantitatively: its amplitude (magnitude).