A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Harmonic wave equation and Newton's second law
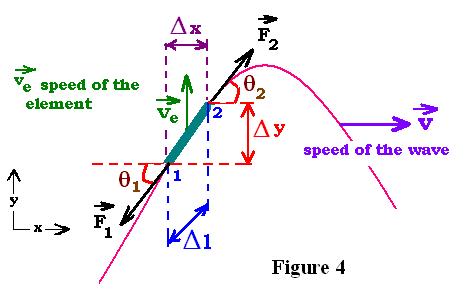
Let's consider a string wiggled once in the (xy) plan from its equilibrium
position. The wave produced propagates along the + x axis using the string
as a medium. Un element of the string is represented as follows:
This element is bent because of the forces F1 and F2
exerted at the two ends of this element by the two neighboring elements.
We assume that the disturbance is small, such that the force F called a
tension along the string is uniform (F = F1 = F2);
and the slope of the string is not large (the angles θ1 and θ2
are small; that is the wavelength λ >> the amplitude A of the wave ).
The net force on the element is :
ΣF = F1 + F2 = (F1x + F2x, F1y + F2y) (1)
Its x-component is: F1x + F2x = F(cosθ2 - cosθ1). As θ is
small, we can use the Mac-Laurin series cosθ = 1 - (1/2) θ2 + ... and consider just the
first term wich is 1, to find that component is null.
It remains then the y component of the net force.
F1y + F2y = F(sinθ2 - sinθ1) =
F(tanθ2 - tanθ1) ( θ is small)
But tanθ is the slope of the function at the point x, that is ∂y/∂x. So
tanθ2 - tanθ1 = [∂y/∂x]2 - [∂y/∂x]1 =
Δ[∂y/∂x] = (Δ[∂y/∂x]/Δx) Δx = (∂2y/∂x2) Δx
Then:
F1y + F2y = F (∂2y/∂x2) Δx (2)
If the mass of the string is M and its length is L, the linear mass density μ ; that
is the mass per unit length is μ = M/L. The related mass of the element is m = μ Δ x.
The Newton's second law for the element is:
ΣF = m (∂2y/∂t2)
It becomes:
F (∂2y/∂x2) Δx = μ Δ x (∂2y/∂t2)
Thus:
(∂2y/∂x2) - (μ/F) (∂2y/∂t2) = 0
(3)
Equating this equation with the wave equation (4.3), we obtain:
(μ/F) = 1/v2. Then:
v = [F/μ]1/2 (4)
The speed of a wave depends on the mass of the medium where this
wave moves along.
©: The scientificsentence.net. 2007.
|
|
|