Algèbre linéaire et
vecteurs
Algèbre linéaire
Exercices
Plan dans l'espace
Droite dans l'espace
|
Mathématiques 3: Algèbre linéaire
Dépendance des vecteurs
1.Combinaison linéaire
Soit E un K-espace vectoriel.
Définition 1
Soient v1, v2, .. ., vp, p > 1 vecteurs d’un espace vectoriel E.
Tout vecteur de la forme:
u = λ1 v1 + λ2 v2 + ··· + λp vp
(où λ1, λ2,. .. , λp
sont des éléments de K) est appelé combinaison linéaire des vecteurs v1, v2,. .. , vp.
Les scalaires λ1, λ2, .. .,λp
sont appelés coefficients de la combinaison linéaire.
Définition 2
Une famille {v1, v2,. .. , vp} de E est une famille libre ou linéairement indépendante
si toute combinaison linéaire nulle:
λ1 v1 + λ2 v2 + ··· + λp vp = 0
est telle que tous ses coefficients sont nuls, c’est-à-dire
λ1 = 0, λ2 = 0, .. . λp = 0.
Dans le cas contraire, c’est-à-dire s’il existe une combinaison linéaire nulle à coefficients
non tous nuls, on dit que la famille est liée ou linéairement dépendante. Une telle combinaison
linéaire s’appelle alors une relation de dépendance linéaire entre les vj.
2. Exemple
2.1. Exemple 1
Pour des vecteurs de Rn , décider si une famille {v1,. .. , vp} est libre
ou liée revient à résoudre un système linéaire.
Dans l'espace vectoriel R3, considérons la famille
{ , , 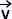 , , 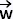 }, avec }, avec
 = (1, 2, 3), = (1, 2, 3),
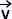 = (4, 5, 6) , et = (4, 5, 6) , et
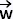 = (2, 1, 0) = (2, 1, 0)
On souhaite déterminer si elle est libre ou liée. On cherche des scalaires
(λ1, λ2, λ3) tels que:
λ1 +
λ2 +
λ2 +
λ3 +
λ3 = = 
ce qui équivaut au système :
λ1 + 4λ2 + λ3 = 0
2λ1 + 5λ2 + λ3 = 0
3λ1 + 6λ2 = 0
les calculs de la réduction de Gauss sur la matrice associée au système
permettent d'arriver au système équivalent suivant:
λ1 - 2λ3 = 0
λ2 + λ3 = 0
Ce système a une infinité de solutions. En prenant par exemple λ3 = 1,
on obtient λ1 = 2 et λ2 = - 1.
La famille
{ , , 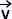 , , 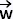 }
est donc une famille liée. }
est donc une famille liée.
2.2. Exemple 2
Dans l'espace vectoriel R3, considérons la famille
{ , , 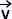 , , 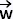 }, avec }, avec
 = (1, 1, 1), = (1, 1, 1),
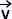 = (2, - 1, 0) , et = (2, - 1, 0) , et
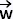 = (2, 1, 1) = (2, 1, 1)
On souhaite déterminer si elle est libre ou liée. On cherche des scalaires
(λ1, λ2, λ3) tels que:
λ1 +
λ2 +
λ2 +
λ3 +
λ3 = = 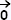
ce qui équivaut au système :
λ1 + 2λ2 + 2λ3 = 0
λ1 - λ2 + λ3 = 0
λ1 + λ3 = 0
les calculs de la réduction de Gauss sur la matrice associée au système
permettent d'arriver au système équivalent suivant:
λ1 - 2λ3 = 0
λ2 + λ3 = 0
On résout ce système et on trouve comme seule solution λ1 = 0, λ2 = 0,
λ3 = 0.
La famille
{ , , 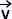 , , 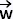 }
est donc une famille lible. }
est donc une famille lible.
3. Interprétation géométrique de la
dépendance linéaire
• Dans R2, deux vecteurs sont linéairement dépendants si
s’ils sont colinéaires. Ils sont donc sur une même droite vectorielle.
• Dans R3, trois vecteurs sont linéairement dépendants si et seulement
s’ils sont coplanaires. Ils sont donc dans un même plan vectoriel.
4. Famille génératrice
Soit E un espace vectoriel sur un corps K.
Soient v1,. .. , vp des vecteurs de E. La famille {v1,. .. , vp} est une
famille génératrice de l’espace vectoriel E si
tout vecteur de E est une combinaison linéaire des vecteurs v1, .. ., vp.
On dit aussi que la famille {v1, ... , vp} engendre l’espace vectoriel E.
Exemple :
Dans l'espace vectoriel R3, la famille de E = R3
{ , , 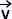 , , 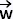 }, avec }, avec
 = (1, 0, 0), = (1, 0, 0),
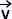 = (0, 1, 0) , et = (0, 1, 0) , et
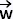 = (0, 0, 1) = (0, 0, 1)
est génératrice car tout vecteur 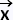 = (x, y , z) de R3
peut s’écrire; = (x, y , z) de R3
peut s’écrire;
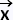 = λ1 = λ1 +
λ2 +
λ2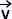 +
λ3 +
λ3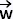
Les coefficients sont ici λ1 = x, λ2 = y, λ3 = z.
|
|