Algèbre linéaire et
vecteurs
Algèbre linéaire
Exercices
Plan dans l'espace
Droite dans l'espace
|
Mathématiques 3: Algèbre linéaire
Les matrices
Matrice inverse
Matrice inverse par les transformations
élémentaires sur les lignes
Matrice inverse par les transformations
élémentaires sur les lignes
1. La technique :
Voici une autre méthode qu'on utlise pour trouver la matrice inverse
d'une matrice régulière, en employant uniquement des transformations
élémentaires sur les lignes:
Voici la technique :
À partir de la matrice augmentée [A|I], on fait des transformations élémentaires
sur les lignes pour aboutir à une nouvelle matrice augmentée [I|B]. La matrice
B est alors la matrice inverse cherchée A-1.
[A|I]  [I|A-1] [I|A-1]
2. Exemple:
| A = |
 |
1 | 0 | - 1 |
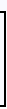 |
| 2 | -1 | 1 |
| 0 | -2 | 1 |
|
La matrice inverse a la forme suivante:
| A-1 = |
 |
x11 | x12 | x13 |
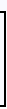 |
| x21 | x22 | x23 |
| x31 | x32 | x33 |
|
En effectuant le produit: A A-1 = I , on aboutit à
3 systèmes d'équations linéaires. Systèmes consistants de trois équations
à trois inconnues.
On peut donc résoudre ces trois systèmes. Plus rapidement,
on procède de la façon suivante:
On construit une matrice augmentée [A|I3] d'ordre 3 x 6 suivante :
 |
1 | 0 | - 1 |
1 | 0 | 0 |
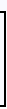 |
| 2 | -1 | 1 |
0 | 1 | 0 |
| 0 | -2 | 1 |
0 | 0 | 1 |
En effectuant les transformations élémentaires suivantes
sur les lignes: L2 - 2L1, - L2, L3 + 2L2, (-1/5)L3,
L1 + L3, et L2 + 3L3, on obtient:
 |
1 | 0 | 0 |
1/5 | 2/5 | - 1/5 |
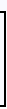 |
| 0 | 1 | 0 |
- 2/5 | 1/5 | - 3/5 |
| 0 | 0 | 1 |
-4/5 | 2/5 | -1/5 |
On a donc :
| A-1 = |
 |
1/5 | 2/5 | - 1/5 |
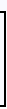 |
| - 2/5 | 1/5 | - 3/5 |
| -4/5 | 2/5 | -1/5 |
|
|
|

 [I|A-1]
[I|A-1]