Mathématiques 3: Algèbre linéaire
Les matrices
Opérations sur les matrices
1. Définitions
1. Comparaison de deux matrices
Deux matrices A = [aij]m x n et
B = [bij]p x q sont égales si et
seulement si:
• elles sont de même ordre : m = p et n = q,
• tous les éléments homologues sont égaux:
aij = bij pour tout i et tout j.
On note A = B
On peut aussi définir une relation d'ordre, c'est à dire une
inégalité dans l'ensemble des matrices.
Une matrices A = [aij]m x n et plus petite
qu'une matrice B = [bij]p x q si et
seulement si:
• elles sont de même ordre : m = p et n = q,
• tous les éléments de A sont plus petits que leurs
homologues dans B :
aij ≤ bij pour tout i et tout j.
On note A ≤ B .
On peut aussi définir: A < B , A ≥ B , ou A > B .
Si la relation d'égalité ou d'inégalité n'existe pas entre
deux matrices, on dit alors qu'elles ne sont pas
comparables.
2. Addition de matrices
Pour faire la somme de deux matrices, il faut d'abord
qu'elles soient du même ordre.
La somme d'une matrice A = [aij]m x n et
d'une matrice B = [bij]m x m est une matrice C
= [cij]m x m telle que
cij =
aij + bij.
C'est à dire la somme termes à termes des éléments homologues;
c'est à dire qui occupent des positions semblables dans leurs matrices respectives.
A + B = [aij + bij]m x m
3. Multiplication d'une matrice par un scalaire
La produit d'une matrice A = [aij]m x n
par un scalaire k est une matrice C
= [cij] m x m telle que cij =
k aij .
C'est à dire le produit de tous les éléments de A par le
scalaire k.
k A = [k aij]m x m
En utilisant en même temps des opérations d'addition et de multiplication
par un scalaire sur des matrices, on réalise ainsi une combinaison linéaire de ces matrices.
4. Produit de deux matrices
Le produit matriciel d'une matrice A = [aij]m x p
par une matrice B = [aij]p x n est une matrice C
= [cij] m x n telle que cij =
Σk =1,p aikbkj .
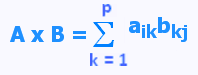
On remarque que:
• Le nombre de colonnes de A doit être égal au nombre de lignes de B.
L'ordre de la matrice produit C m x n est égale au produit
du nombre de lignes de A et du nombre de colonnes de B.
• Sauf si les matrices son carrées, si A x B est possible , B x A
ne l'est pas.
• Le carré A2 d'un matrice A est toujours possible.
5. Propriétés des opérations sur les matrices
Toutes les propriétés des opérations sur les nombres réels
sont aussi valides pour les opérations sur les matrices, sauf (3):
• En général, la commutatvité du produit :
A x B ≠ B x A
• La simplification avec le produit :
A x B = A x C  B = C B = C
• L'existence des diviseurs de zéro :
A x B = 0  A = 0 ou B = 0 A = 0 ou B = 0
|